Last week we took a look into the Asirikuy PA system repository and how the correlation between in-sample (IS) and real out-of-sample (OS) Profit Factor (PF) values changed as a function of the group of systems we looked at. This week we are going to be doing the same exercise looking at the IS/OS Sharpe ratio (SR) values of the repository in order to evaluate how the Pearson correlation of these values change as a function of different group selections among systems above a given trade threshold. I would also like to point out that the Pearson correlation is probably not an ideal metric for this analysis due to the variations in group size when changing among different percentile groups – except for groups where the number of points is similar – so although this analysis is indicative a more robust approach would probably use something like the Spearman’s rank coefficient (thanks to Fd for the suggestion). I will explore using this coefficient within a later blog post.
–
–
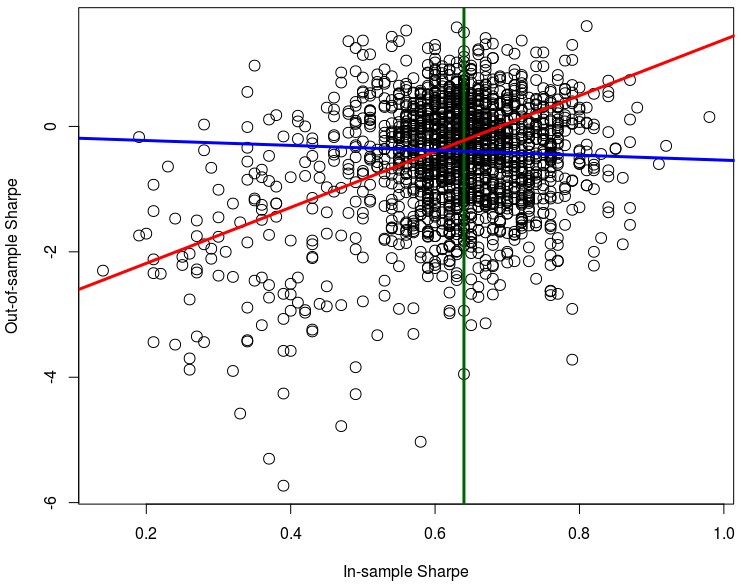
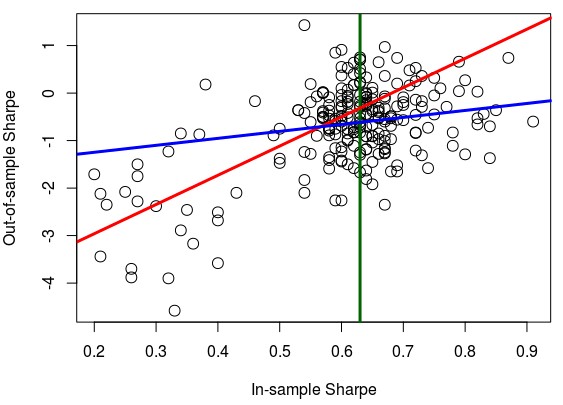
In the case of the Sharpe ratio for systems with more than 100 trades – first graph above – we find that the correlation between IS/OS values is higher (0.39) for systems below the 50 percentile line (in green) and lower for systems above it (-0.006). The red line shows you a linear regression of the systems to the left of the green line while the blue line shows you a linear regression for systems to the right of the green line (the number of systems in both groups is fairly similar, 870 vs 810 points). As it was the case with the PF, in the SR we see that as we go to higher IS values a proportional increase in the OS SR becomes less and less guaranteed. However if we analyze only systems with more than 200 trades – second image above – we do notice an increase in both linear regression lines with the R values changing to 0.63 (red) and 0.14 (blue). This is a significant increase from the values seen in the 100 trade threshold, showing that with an increase in the number of trades we continue to see an increase in the IS/OS correlation, even if the correlation is indeed much weaker for larger IS values.
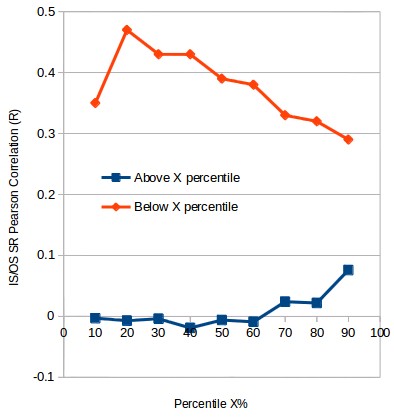
Repeating the analysis we did before using different percentile values – image below – we see the same pattern as in the case of the PF. In this case we see that when looking below the lowest percentiles the correlation is initially higher and drops continuously as we look below increasingly high percentile values. This again points out to a deterioration of the correlation between IS/OS values as we include higher IS SR values. When doing the opposite exercise and looking at values above these percentiles we see that the correlation remains small most of the time and actually starts to increase as we move towards the highest SR values. This is interesting as it points out that increases in the IS SR are more likely to lead to increases in the OS SR at the highest SR values, although much smaller than in the case of the smallest IS SR values. However since the highest percentiles are made up of much smaller groups it is very probable that this small increase in correlation arises merely due to random chance when looking at increasingly small groups.
–
–
This analysis again points out to a limit in the increases in OS SR performance that can be achieved by pushing up the IS SR. It seems clear that pushing up the 30 year IS SR indefinitely does not seem to lead to ever increasing values in the OS SR. This may be related to the fact that pushing the IS SR higher requires higher complexity in the algorithms used which leads to difficulties in the proper evaluation of bias sources and can lead to increases in curve-fitting bias. This becomes necessary when pushing Sharpe ratios above certain thresholds since we might be demanding a level of performance that might be achieved much more probably from bias sources than from true market inefficiencies. Contrary to the profit factor we have used the Sharpe ratio as an explicit filter when mining, reason why we have are now accumulating systems only with a SR above 0.5 (the reason why there are so few samples below an IS SR of 0.5).
What these PF and SR analysis show us is that increases in trade number tend to show increases in IS/OS variable correlations but most of these gains are related to lower PF and SR values. This again points to the fact that there is an optimum upper threshold of SR and PF values to demand when searching for systems and searching for higher values is not something that will be rewarded in the OS by the market. This helps explain why trading is not merely a computational strength problem – the ability to search for the better IS inefficiencies – but a problem that is both related with the complexity of what is searched for and the performance that is demanded. Try to get things that are at the top percentiles of IS potential performance and your chances of being disappointed will increase exponentially. This might lead us to think that if you limit system complexity and degrees of freedom you might have a better chance at achieving positive results, although that is also a topic for a future blog post — repeating the above analysis as a function of complexity.
–

–
With the above it seems clear that the search for IS/OS correlations is neither linear nor simple. Finding ways to increase OS performance depends on much more than having control over IS statistical variables and demanding the very best systems – this is actually counterproductive – it instead depends more on being able to attempt to predict what the future holds with whatever IS/OS relationships can be observed in past periods. Machine learning offers us a very powerful tool to attempt to do this, although it can also be plagued with sources of statistical bias and similar issues that have to be properly addressed. If you would like to learn more about our PA portfolio and how you too can trade systems, even using ML algorithms that attempt to predict OS performance please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading.




