Mechanical Forex

When we want to use trading systems one of the most important things we need to know is how “good” or “bad” each system is. Although the concept of system quality cannot be reduced to a single set of variables as it pertains to areas as diverse as draw down, profitability, draw down duration and inherent simulation robustness we can come up with certain calculations that give us some idea of how one system compares with another in several of the above mentioned areas. On today’s post I am going to discuss the use of Monte Carlo (MC) derived calculations to measure system quality against those obtained directly from simulations. Are these variables better candidates to compare our systems?

If you have been following this blog or Asirikuy for a while you’ll notice that our chief way to compare systems is through the use of the average compounded yearly profit to maximum draw down ratio derived from simulations as well as some other characteristics which are derived from draw down period lengths and depths such as the Ulcer and Pain Indexes. Up until now these variables have allowed us to compare one system against another but as time has progressed we have seen some of the weaknesses which arise from using results which are only based on “one set” of simulations.

–

–

A given simulation usually has a set of statistical characteristics which can turn out to be an “excellent case” during the backtesting period. For example you can have a system which gives very high profit Vs draw down characteristics because the past 10 years results for this particular combination were “extremely good”, however an in-depth analysis of the real “rainbow” of possibilities which arise from the application of Monte Carlo simulations may reveal that the actual profit and draw down levels which are to be expected are far less than those obtained through that single simulation set. Therefore this rises the question of whether or not it might be better to simply use the characteristics derived from Monte Carlo simulations which arise from an extended Monte Carlo analysis of the distribution obtained from the simulations.

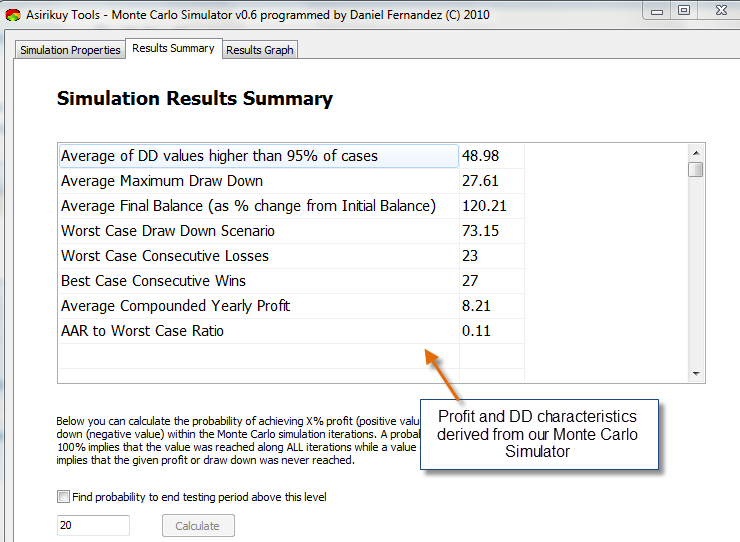
The idea here is to take a distribution derived from a simulation to run an MC simulation that spans a wide array of iterations (usually 100K) over the expected number of trades within the backtest. After obtaining the results for this simulation we calculate the worst draw down amongst all iterations as well as the average compounded yearly profit obtained in average and use it to derive an average compounded yearly profit to Monte Carlo Worst Case draw down ratio which enables us to have a better comparison of our systems against one another. This in fact allows us to gauge the quality of the distributions themselves against a wide array of possible individual outcomes instead of a single outcome which might have been a rarely “good” case of the distribution.

Certainly this also raises the point of addressing other criteria in the same way. For example we can evaluate Ulcer and Pain Index proxies (as there is no time variable in MC simulations) which can be derived from the 100K iterations instead of our single simulation results. Additionally we can also perform some “bashing” of the distribution in order to take into account things such as broker dependency as execution problems. We could introduce a random negative distortion against a given percentage of trades which could show us a more realistic perspective of what might happen in case we use the systems on a broker which gives worse results than the simulation. This adds another layer of robustness as we would be able to see a little bit better how our system would behave if a given number of trades have either opposite or worse-than-expected outcomes. This will certainly be an interesting experiment to evaluate our systems in virtue only of MC simulations with the distributions derived from the original backtests.

The first few experiments I have done in this regard reveal that the MC simulation derived variables do give a more realistic picture of the systems we are trading and they become extremely important for portfolios where the effect might be more pronounced. A portfolio might have an expected yearly profit from simulations of 120% which becomes 90% on Monte Carlo simulations because the case of the original simulation was simply a very optimistic outcome of the true distribution dispersion of the simulation technique. The distance between the simulation’s maximum draw down and the MC Worst Case draw down – as I mentioned on a previous article – is also a proxy for system robustness and gives us an idea of how good a system behaves in this regard. Systems that have a robust design tend to have simulation draw down scenarios close to the MC Worst case one while more potentially curve-fitted strategies tend to have more distant worst cases.

In the end I believe that system quality and comparison might be better deduced purely from a MC analysis as this circumvents a few problems which are not seen on the original single backtest. Perhaps the most useful aspects also pertain to the ability to see the likehood of different scenarios such as the probability to reach a certain profit or draw down scenario within the MC simulation. Through this analysis we are bound to have a much more realistic comparison between our systems, especially when we subject them to additional stress in simulations such as that caused by the random worsening of results or a random scattering of results aimed at simulating broker dependency.

If you would like to learn more about our systems and how you too can carry out Monte Carlo simulations of your own strategies please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading in general . I hope you enjoyed this article ! :o)