Mechanical Forex

During the last month we have discussed several ways in which we can discover whether a strategy has reached a worst case scenario based on Monte Carlo simulations. We have gone through the evaluation of worst case statistics at different period lengths and we have also discussed the use of functions to automatically calculate the worst case values for the sharpe and CAGR according to a system’s last drawdown period length and statistics since the drawdown period’s start. Today I am going to show you how to perform a much more graphical analysis using the qq-pat library so that you can easily discover whether your system has breached or is close to breaching a worst case. After reading this article you’ll have a powerful tool at your disposal to easily tell if your system is behaving within expectations or if it is behaving erratically. No more sweating, doubting and second guessing. To reproduce the images you see within this post please download these files.

–

import pandas as pd
from pandas_datareader import data
import datetime
import qqpat
import csv

def lastValue(x):
    try:
        reply = x[-1]
    except:
        reply = None
    return reply

tradeTimes = []
tradeBalance = []

with open("sys.txt", 'rb') as csvfile:
        reader = csv.reader(csvfile)
        i = 0
        lastBalance = 100000
        for row in reader:
            if i > 0:
                tradeTimes.append(datetime.datetime.strptime(row[3], '%d/%m/%Y %H:%M'))
                tradeBalance.append(float(row[10]))
            i += 1
                                     
data = pd.DataFrame(data=tradeBalance, index=tradeTimes).resample('D', how=lastValue).pct_change(fill_method='pad').fillna(0)

analyzer = qqpat.Analizer(data, column_type='return', titles=["sys"])

analyzer.plot_mc_limits(iterations=100, confidence=99)

–

One way to use Monte Carlo simulations to assess whether a strategy is behaving as expected is to measure the expected distribution of some statistical property and then compare whether the value of that property for the trading system being traded is worse at a given confidence interval within the current drawdown period. If 99% of cases within a Monte Carlo simulation have a minimum Sharpe of -2 after a 200 day drawdown period and your strategy is currently facing a Sharpe of -3 during this same time then you could say within a 99% confidence that your system is not working anymore. However this has the problem that statistics are usually hard to visualize and calculating these statistics does not give you a sense of when the strategy actually breached the worst expected behavior at your chosen confidence level. To solve these problems I have implemented the plot_mc_limits function in qq_pat.

The plot_mc_limits function uses a different and tremendously useful property of Monte Carlo simulations that we can use to determine worst case boundaries. Since each iteration in a Monte Carlo simulation actually produces a return series we can not only calculate distributions of statistics at different points in time but we can actually calculate distributions of expected balance values after any given time period. Using this characteristic we can effectively evaluate what our expected worst case balance at any given point in time should be at a desired confidence interval. This means that we can create a bounded plot starting at the last equity high for a trading system where we can project the best and the worst possible case at a desired confidence and the average from the expected cases.

–

–

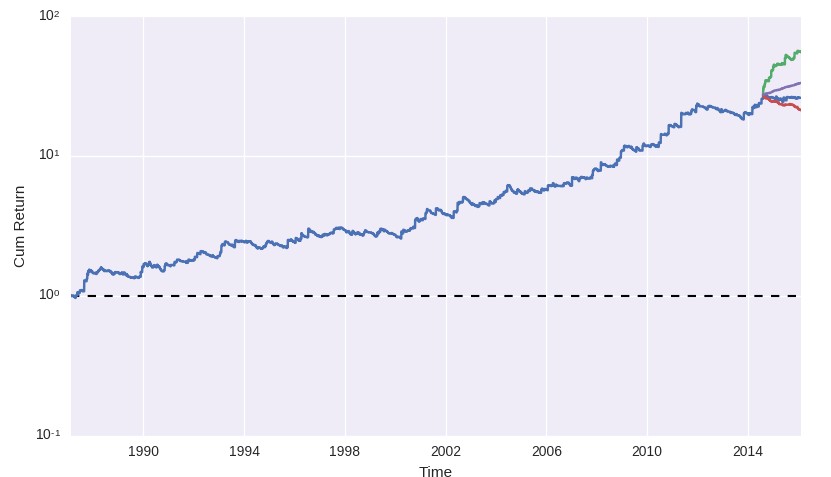
The image above shows you the plot obtained by using the plot_mc_limits function. The red line represents the worst case at a 99% confidence while the green line represents the 99th percentile best case within the monte carlo iterations for each point within the drawdown period. Note that these are not the best and worst equity curves from the MC simulation at these confidence intervals but instead the best and worst points from the distribution of all potential balances at each point in time within the drawdown. For example to get the value after 10 days you form a distribution of all balance values from all iterations at day 10 and you calculate the 99th percentile worst and best values to draw the point in the graph. You can see that the lines start right at the last equity high – which is when we are interested in starting to evaluate a worst case scenario – and they continue to evolve up to the last point in the system’s equity curve. Of course the MC iterations are done using only the returns before the last equity high.

The benefits of an analysis like this are quite instantaneous. You get a very graphic description of whether your strategy is failing or not without having to perform any additional calculations. You can see how close or how far away your strategy is an has been from its worst case since the start of the current drawdown period and you can instantly tell whether you should be watching the strategy more carefully or not. The image below shows a zoom into the drawdown period for the plot showed above, you can see that despite the fact that the strategy has been within a drawdown period for around 6 months the balance curve has always been above the worst case points for the strategy. If the strategy was not behaving as expected it would have come much closer or would have even breached the red line. You will notice that as the drawdown period grows longer for a strategy like this the red line will start to flatten and to eventually go up, that is because there is always a point for a system with a positive expectancy when the worst case expectation is a profitable outcome, drawdown periods can never be indefinite for a strategy that is expected to produce a return.

–

–

If you want to use this it is just a matter of loading your strategy’s backtesting results into a pandas array and then use qq-pat function to create the above plot at your desired number of iterations and confidence interval. Using the library you can even automate the creation of these graphs after running a back-test and you can go even further and automate the detection of a worst case breach at any given point in time. Right now I am implementing this within our GUI back-testing result analyzer at Asirikuy so that our members can also have easy access to these graphs without coding. If you would like to learn more about worst case evaluation and how you to can learn many ways to detect system failure please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading.