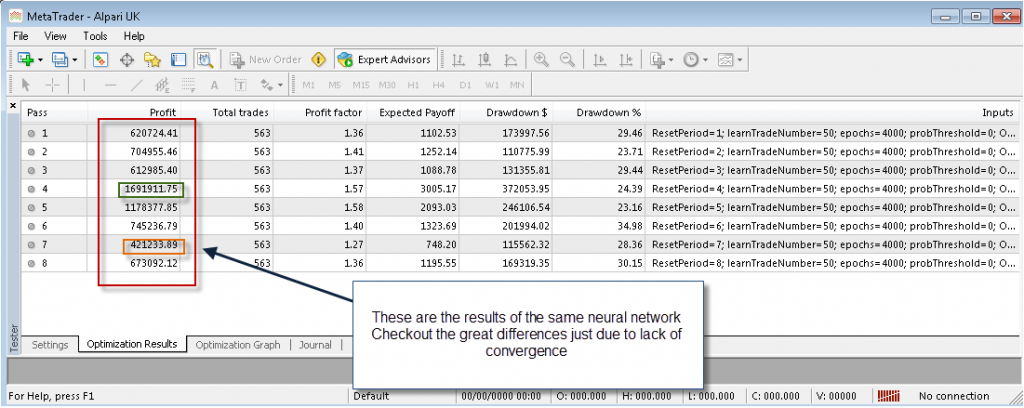
Through my “neural networks in trading” series of posts I have talked about many issues surrounding the use of neural networks in algorithmic trading including the creation of stand-alone NN systems and the use of neural networks as ways to improve other aspects of strategies (such as money management). Today I am going to be talking about a serious issue any trader attempting to implement neural networks solutions can face which has to do with the fact that neural network solutions need to converge in order to be useful. I will be giving you some hints on how you can reduce and almost completely eliminate this problem and – more importantly – how you can see if your neural network solution suffers from this very bad case of “indecision”.
A big problem with any neural network solution is that it relies on the training of a given set of functions (neurons) to fit a given set of output data starting from some random weights. Since the starting point of the network is random the training procedures can have different outcomes and this leads to the problem that the same network can be trained twice on the same data to give completely different out-of-sample results. This is of course a very important problem since the neural network could be giving good results that are just randomly being generated which are then totally different when the neural network is run for a second time. How could you know that your NN works if it can give seemingly any result ?
–
–
A well built neural network solution eliminates the above problems through two main ways. First of all the use of neural network committees instead of single networks becomes a priority (as usually a decision taken by a group of networks is more convergent) and using an error threshold and epoch number which is high enough as to provide enough convergence for the networks. However the are several instances where this is not enough, particularly when the neural network decision affects future training sets. For example when using a neural network MM approach which modifies position sizes a small divergence in the beginning of the test between two separate back-tests can cause an increasing effect which in the end can lead to dramatically different outcomes. This is why self-correcting ideas have a much harder time at reaching convergence.
If you’re doing a neural network implementation where the outputs of the network will affects its future inputs then the problem can be fixed by keeping a “phantom copy” of what the outcomes without intervention would have been so that deviations in the test will not be magnified in the future by small differences attained by the network committees (there are some other creative solutions to this problem). Once you do this your neural networks will most likely converge much more towards usable solutions. You should also always consider the amount of epochs, errors thresholds and inputs you’re using as if your inputs and outputs are not correlated or if your epoch training is not enough you may find that convergence doesn’t happen despite some of your other efforts.
As you see the building of neural network solutions is not easy and great care must be taken to analyze and take into account all aspects that could hint at the fact that the neural network is simply doing its job due to random chance. Always run at least 20 tests of your neural network implementation over the same data and determine the standard deviation of the relevant resulting parameters in order to see how your neural network is behavind regarding convergence and reproducibility. It also helps to code UI Components so that you can get the error values and training set convergence results to see if your epoch choice is adequate.
If you would like to learn more about my work in algorithmic trading and how you too can learn more about the world of mechanical trading and the building and evaluation of systems please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading in general . I hope you enjoyed this article ! :o)