When you build a trading system one of the most common challenges you encounter is the definition of entry and exit conditions. For most systems, this condition is given by the breakout of some threshold value which has to be defined through an optimization procedure using hindsight (could be long term optimization or validated optimization using WFA). The definition of this criteria by optimizations and the very nature of the way in which systems trade, opens up the way to several problems including the validity of the defined thresholds as well as the inherent broker dependency created by the binary signalling structure. Today I am going to discuss the implementation of fuzzy logic in trading systems using an approach that avoids lot size granularity problems, opening up the way to another trading mechanism for algorithmic strategies.
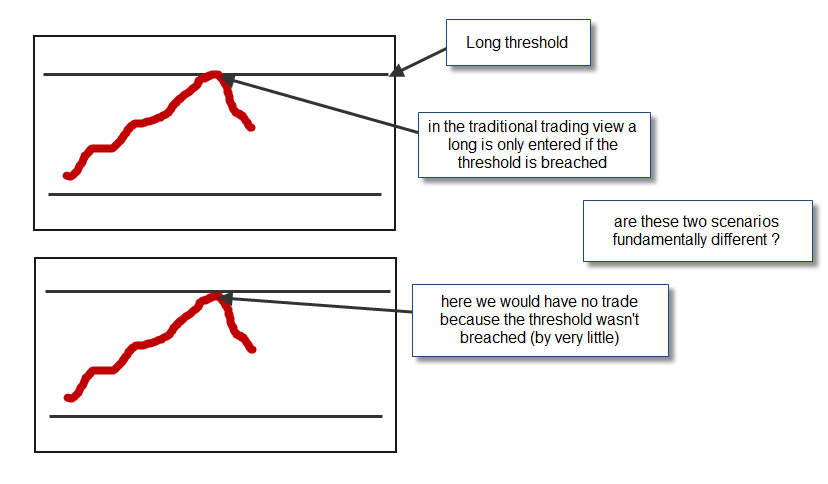
Let us suppose you have a trading system that trades based on an oscillator, this oscillator gives signals from 0 to 100 and your system enters short trades whenever the oscillator crosses the 20 line and long trades whenever the system crosses the 80 line (note that I am using these values as examples, they could be any values). There are several problems inherent to the way in which this trading logic is formulated. First of all, the definition of lines 20 and 80 is arbitrary and leads to clear “black and white” decisions. Whenever the strategy is below 80 the probability to enter a long trade is zero and whenever the oscillator is above this line the probability to enter the trade is 100% (and vice versa for short trades). The first consequence of this is that if we reach a level of 79.9 on one broker and 80 on another, then the signal will be entered on the broker that reached 80 but not on the other. Does this sound right ?
–
–
The problem with binary trading decisions is that there is always a logical problem because in trading there is no dramatic change from black to white when you go from 79.9999 to 80. Why is a trade at 80 valid while a trade at 79.999 is not ? The reason why we choose the 80 is generally because – in historical tests – the 80 gives a better result than the 79. However – even if you included 79 – the problem would still continue as why would a 79 be different from a 78.99999? The problem is that there is a clear-cut boundary between what can be traded and what cannot be traded, a boundary that has no clear base in reality. From a natural perspective, the decision to take a trade is very clear at some point and more difficult to make at another but there is no clear boundary where these conditions take place.
Picture the same system used in a discretionary way by a regular trader. If the trader sees a 79.999 he may still enter the trade because the technical scenario looks the same as if an 80 had been reached, however at 79 the trader might start to have some doubt but he/she might still enter the trade because the technical scenario still looks similar. However at a value of 60 the trader will not risk entering a trade because the picture is very different in this case. How can we reflect doubt and gradients in the trading of strategies? How can we make an algorithmic strategy behave in a way that is consequential with the reality of the market it’s trading?
The first answer – which I had already mentioned in a post about fuzzy logic in the past – is to build a system that doesn’t decide at a clear boundary but makes incremental trading commitments as the area where a decision is clear is approached. For example a system may trade a risk of 0.1% if the value of the oscillator is 75, then 0.2% if its 76 and so on until it reached the final desired risk – let’s say 1% – if the trade reaches the point where there is certainty about the technical scenario (>80). However the problem here is that playing with the lot size introduces problems dealing with granularity that can greatly complicate the management of trading positions, especially when the amount of capital is limited. An additional complication is that you would need to handle several simultaneously open positions and you would also need to handle which ones to close/open as the technical scenario evolves. In general I tried to implement this approach but decided against it because it adds a lot of complexity to a problem that shouldn’t be so complicated. As in most management cases, the granularity problem was the biggest obstacle to its successful implementation.
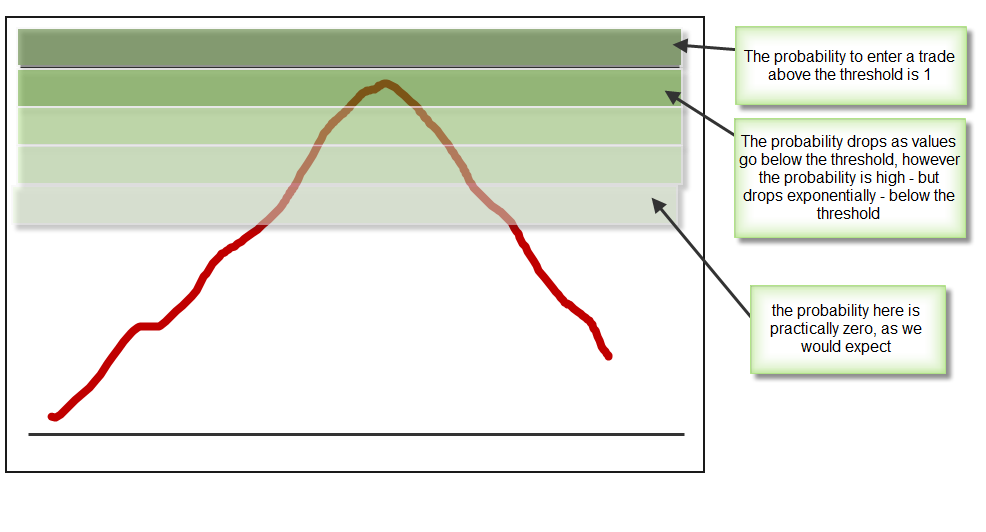
My next idea has been to implement fuzzy logic in a way that preserves the amount of capital risked per trade – no playing with the lot size – but instead we introduce a random component around the trading decision element. As in the case of a discretionary trader, we create doubt regarding technical scenarios that are below the threshold boundary while we reinforce scenarios that are at or above our desired level. In this case what we do is give the technical scenario a score based on the difference between the threshold and the oscillator value (using a normalized exponential function that ranges between zero and one) and we then make a “coin toss” using a random number generator that decides whether we take the trade or not. For example if the threshold is 80 we will give this value a score of 1 and scores will decay exponentially as they move away from this threshold. If the value of the oscillator is 79.999 its score will be very close to 1 and therefore the probability to enter a trade will be very high. However, if the oscillator is 70 the probability will be quite low because the value is already far away from 80. Nonetheless, the probability to trade will still be existent, although tremendously low.
I would also like to point out that the above element of randomness is nothing to be afraid of. Trades would still match on signals that we would consider “traditional” (any move above 80) but the signals that are close to 80 but not 80 still have a chance to be traded when previously they were never going to be traded. This introduces an element of realism into the system because it acknowledges the gradient in technical clarity between a clear boundary and a value which is close but not exactly above it. With this new technique we see the technical scenario as a “fading entity” whose clarity decreases as we go away from the boundary, we can never make a distinction between when things are black or white but we evolve through an array of greys.
–
–
This implementation of fuzzy logic allows you to trade without any binary choices. It can be implemented inside breakout strategies, price action based systems, cross overs, etc. Any trading system that currently makes its decisions based on some binary outcomes (either its black or white) can be modified to use this fuzzy logic approach. Currently I am testing this in a few Asirikuy strategies and will come back with my findings in a future post. Additionally it is important to realize that you can also remove threshold limitations if you take into account the natural properties of indicators (for example you can choose oscillator threshold as 0-100 which are the only values that would imply 100% certainty), this allows to build thresholds without the need for optimizations.
If you would like to learn more about trading strategy development and how you too can implement your own trading systems please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading in general . I hope you enjoyed this article ! :o)





Hi Daniel,
although I think fuzzy logic can help to build a strategy which takes into account a variety of influencing factors, I don’t think that fuzzy logic is a way do circumvent binary decisions. Any program running on a binary machine can’t do anything else than binary decisions. As you’ve pointed out randomization can help to get out when trapped in an repeating unfavorite situation, however this is nothing proprietary to fuzzy logic. My belief is that Fuzzy logic or neural networks are nothing more than algorithms looking a the same thing from different angles, they are just other formulations of a problem which might be appropriate but do not have to necessarily. It’s all about infering having unknown distributions and conditional probabilities.
Best regards,
Fd
Hi Fd,
Thank you for your comment :o) Although you are right in that fuzzy logic and neural networks are nothing but “looking at the same thing from a different angle” it is in fact true that the fuzzy logic approach tackles some problems that you cannot simply tackle with a normal trading technique based on binary decisions. For example the randomization in potential entries and the “blurriness” of intermediate trading scenarios, causes an effect that can give some insight into the potential problems caused by broker dependency (for example you can see how variations in trading outcomes affect overall system characteristics. In other words, how much does being in the border-line between a clear case and a grey one can affect your outcomes).
I would say that the problem goes beyond “inferring having unknown distributions and conditional probabilities” in the sense that we also tackle other things – such as feed dependency – that a systems should ideally deal with in some way. However I agree with you in that the problem is always the same one, there are just many mathematical tools to tackle it. In this case I suggest fuzzy logic as an additional aid, rather than a way to solve the problem. Thanks again for posting :o)
Best Regards,
Daniel
Hi Daniel,
Thanks, this is a great idea and I will surely try to implement this to my current strategies. However, won’t this simply add another new variable that has to be optimized along with the previous ones. With another variable I mean how quickly the exponential function decays, exp(-k*x), with k the new variable and x the difference between the current oscillator value and the conventional threshold. My professor always says: with enough free variables you can fit an elephant :-) Besides, the argument of the exponential function does not have to be linear in x, it can have a Gaussian shape such as exp(-k*x^2).
What are your thoughts on this?
Regards,
Edward
Hi Edward,
Thank you for your comment :o) You’re right in that you can make the exponential function more complex, you can also fit any parameters as a function of system historic properties (something I would avoid doing). In general I believe the best approach would be to select a decay such that probabilities are close to zero when they should obviously be zero and then make sure they are one when they should. In the above example I would make the exponential fall below 0.01 when the oscillator value is below 60 and then make an exponential such that a value of 1 is reached when the threshold (80) is reached. Definitely this is just something I’m beginning to explore so my opinions could change as time goes by :o) Make sure you share any developments you have with us. Thanks again for posting!
Best Regards,
Daniel
Hi Daniel,
In many of your posts you refer to the necessity of thorough backtest and walkforward analysis of the developed strategy. But wouldn’t the addition of such a random element in the expert advisor make these tests unreliable? Any of these tests would produce different outcomes as a result of the random factor. Surely the effect of the randomness would even out (mathematically) when the sample size reaches infinity, but even with 10 years of backtest data this would not be accomplished? What are your thoughts on this?
Regards,
Marko
Hi Xetar,
Thank you for your comment :o) This is true indeed but it teaches you a lot about your system. The extent to which your system is affected by a random component that affects border-line trades gives you an idea about how much broker dependency you might experience. If you run 30 back-tests with a random component attached to “grey” trade outcomes and you get a 50% variation in profit then this means that a very high percentage of trading outcomes are based on trades that could easily change depending on the broker. Since the probability to trade is always 1 above the trading threshold, a large effect of the random component hints to a possible weakness of the system. Ideally one could take the worst-case scenario achieved from several tests and use this as the projected statistical scenario, however I am currently just researching this so I do not have a very good idea of how to apply it yet. Thanks a lot for commenting :o)
Best Regards,
Daniel