An Asirikuy members sent me an email a few days ago asking about the use of Monte Carlo simulations in Forex trading when systems do not have a single open position but have multiple positions open at the time, potentially with time related correlations between positions. The question came as this user was interested in carrying out Monte Carlo simulations of a strategy that opens up several positions in favour of a trending movements (a pyramiding system). On today’s post I want to answer this question with particular emphasis on why traders need to be very careful when running Monte Carlo simulations of strategies that don’t have simple entry/exit logics. Sampsonievskiy Monte Carlo simulations cannot be made on a “one size fits all” philosophy as some systems require special considerations and modifications when performing this analysis.
For those of you not familiarized with Monte Carlo simulations I will now give a small introduction (although I would advice you to read previous forum posts on this type of simulations). A Monte Carlo simulation attempts to predict the extent to which randomness can affect the outcomes of a trading system while preserving an absolute trade return distribution. In essence we run a simulation where we know what the average distribution of returns for a strategy must be but we distribute these outcomes randomly. If on a back-tests the outcomes were 1-2-3 in the Monte Carlo simulation they can be 3-1-2. This random mixing of returns allows us to perceive worst statistical values for our systems.
–
–
One thing that stands out from the above paragraph is that simple buy modafinil los angeles Monte Carlo simulations rely strongly on the independence of trades. Since you are finding out possible mixes of trading outcomes, outcomes 1, 2 and 3 must be independent so that in real life the outcome 3-1-2 would have made sense as well. For systems in which the entry and exit logic are clearly separated – and there is never more than one trade open at a time – this assumption can be considered to be true. As long as your trading system behaves in a manner that doesn’t explicitly correlate trades, you are going to have a reliable Monte Carlo simulations while following this simple approach.
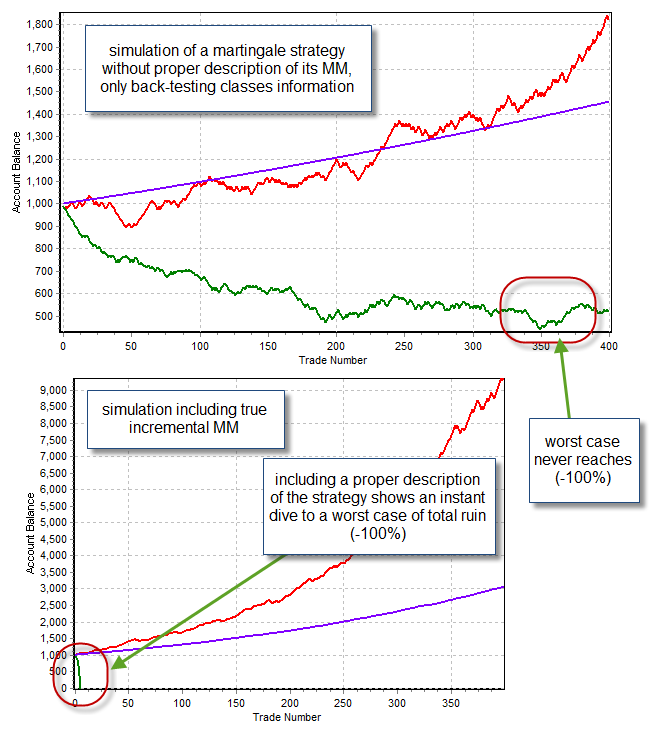
The problem of course, comes when we consider systems where trade outcomes can be correlated somehow. The most extreme case would be a Martingale system where the market exposure of the system is not capped and correlates with the number of consecutive losses. If you run a Monte Carlo simulation based on a back-test for a martingale that hasn’t gone burst, the distribution of returns will show you a very low probability to ruin the account because the true statistical nature of the system is not generated. Include the martingale logic in the MC simulation – the inherent correlation between risk and consecutive losses – and you will find out that in the long term the account will always be wiped clean (the statistical demonstration that martingales always wipe accounts).
However the above analysis also applies to less extreme cases. Let’s suppose you have a system that pyramids positions, opening up new positions as a trend moves on. If the trend reverses, all of the positions will be closed at the same point, implying a correlation between the returns of all of these positions. Using a regular Monte Carlo simulation these correlations will be lost and the risk of consecutive losing trades will be underestimated because the evident correlation between losses is not being reflected. This is especially important if there is no cap in the amount in which positions can pyramid, which creates an effective open cap to market risk. Using Monte Carlo simulations while ignoring explicit correlations is a recipe for the underestimations of risk.
When dealing with cases where the losing/winning nature of positions is evidently tied by the way in which the positions are opened or closed it becomes necessary to include this within the simulation’s code (if a result describing the system wants to be achieved). It is particularly important to do this because MC simulations where these correlations are properly depicted can show up potential flaws in strategy design and testing. A strategy might show very good simulation results – apparently everything has been done precisely – but MC simulations including adequate trade correlations can show huge under-estimations of risk. The inclusion of these correlations can also show how risk and losses can be affected by these trading system features in ways that are not obvious when looking at logic or simulations.
–
–
The way in which the above correlations are included can vary but the true nature of the system must be reflected. For a system that pyramids positions, you can include a basket type logic where n trades are opened at the same time with outcomes correlated in a given manner. However an important thing when doing this is NOT to derive basket return distribution classes from the baskets seen in simulations unless the extent to which baskets can grow is somehow limited. If the formation of baskets is unlimited, the Monte Carlo simulation should include the probability to form unlimitedly large baskets. You can implement this as a gaussian probability centered at the most common basket size in simulations but giving a non-zero probability for baskets even twice as big as those seen in simulations.
In general my advice would be to be very careful with the implementation of pyramiding techniques and the opening of multiple positions because this is always an avenue for losing the cap on market risk. If the possibility of unlimited market exposure exists (however “rare” it might be) then the Monte Carlo simulations also need to reflect this possibility (even if it has never showed up in testing). A good technique to avoid this would be to introduce correlations that never imply increases in risk such as making sure all positions move to at least break-even outcomes whenever a new position is entered. This ensures that baskets- no matter how big – will always represent the same risk level (adequately capped exposure). Remember that unlimited market exposure might not be obvious in simulations but it will eventually show up (as it does for strategies with more obvious cap problems, such as martingale systems).
If you would like to learn more about Monte Carlo simulations and how you too can learn to run simulations for your systems please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading in general . I hope you enjoyed this article ! :o)





Hi Daniel,
one idea to tackle potentially existent autocorrelations in trades would be to calculate conditional probabilities and returns (measured as % of equity) over all trades and use the values obtained as random variables themselves. This way you can do MC simulations under the hypothesis of autocorrelation without needing special user input.
Best regards,
Fd
Hi Fd,
Thank you for your post :o) I think I do not understand what you mean very well. For example in the case of a pyramiding systems, figuring correlations between trades might not be useful because this might still not catch the full risk of the system since stronger correlations outside of what happened in the back-test might exist. What I mean is that taking into account the explicit correlations – the ones used as trading rules – is fundamental because otherwise you will not see the full picture. As I see it you will never get an equivalent to these rules from studying the statistics of the back-test because the explicit correlations are open up to much more risk that what might be contained in the simulations.
However maybe I do not understand well ? Please post an example so that I can better catch your point! Thanks again for posting :o)
Best Regards,
Daniel