On yesterday’s post we looked at the differences that appear when considering different reward to risk scenarios in edge-less trading on the EUR/USD. These results showed us that there has been a historical tendency to favor the 50:100 pip risk to reward scenario on this pair, explaining why this might be such a common source of advice for new FX traders on forums (as more edge-less traders using this position management scheme would have survived). Today we’re going to look at another interesting aspect of edge-less trading that involves the search for huge rewards in the FX market at the expense of using a considerable amount of risk that ultimately jeopardizes the entire trader’s capital. This is a very common scenario for new small retail traders; who often seek to generate huge amounts of profit on a rather small amount of time. We’re going to see why this is not a very good idea and why there are still a significant number of traders who are able to achieve such a feat.
–
–
In order to simulate this scenario I carried out 7891 simulations (2x to check for convergence) using random entries on the EUR/USD 1H charts from 2000 to 2014. Trades were entered with a 10% probability on each hourly candle (if no trades were open) with a symmetric SL/TP of 50 pips (other risk to reward scenarios tested had fairly similar outcomes, with about a +/- 10% deviation) and risked 5% of trading capital per trade. Trading was finished whenever a trader either went broke (balance went to zero) or the trader achieved a profit of 10x the starting capital. The risk of 5% was chosen as lower risk levels failed to generate either scenario (bust or 10x increase) with a significant probability.
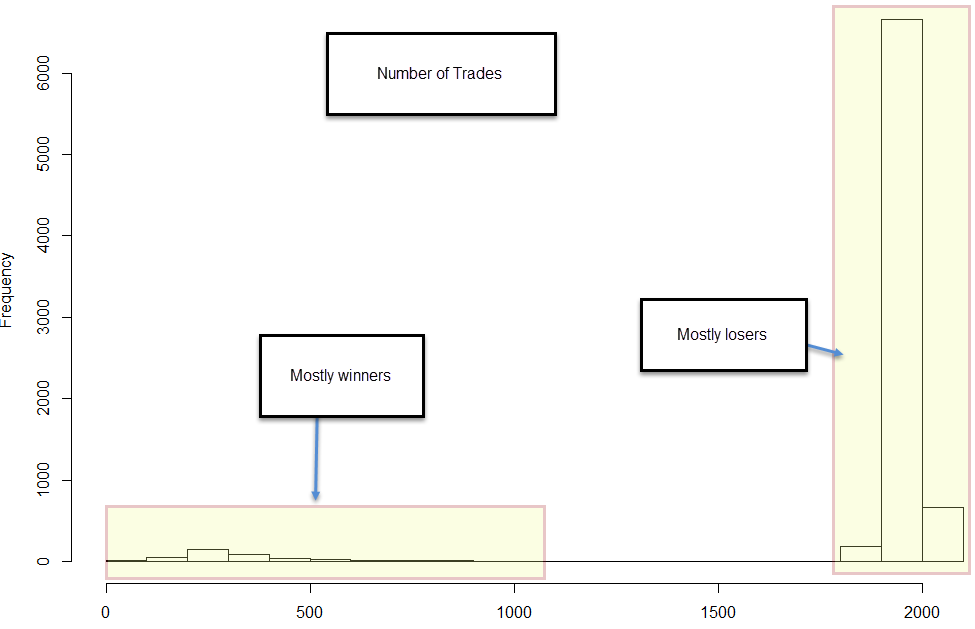
As it is expected, most traders who go broke in the above scenario do not do so quickly but instead follow a negatively biased random walk that allows them to survive for about 60% of the back-testing period most of the time. As you can see on the historgram showing the distribution of trading frequency we have two main distributions that appear (one for mainly winning traders and one for mainly losing traders). Mainly losing traders have a high final trade number (around 1900 on average) while winning traders tend to trade only about 200 trades (note that they stop trading once they reach their target). There are however traders that lose very fast and traders that win after a long series of trades, but such outcomes are not that common. The reason for this is mainly that to reach a 10x target one needs to have a period of rather fast compounding, so this tends to happen rather quickly and during the start of the test when it does reach a successful outcome.
–
–
There are many losers that make a 10x increase in capital sometime within the test but since after going into drawdown reaching a 10x target relative to initial capital may imply a 100x instead of a 10x increase, the probability to achieve the initial 10x capital increase decreases greatly. If a random trader does not reach the 10x increase over initial balance within the first 500 trades then the probability to do so decreases by a factor of 50 since the negative bias imposed by the first 500 trades (3 pips of spread * 500 trades is 1500 pips) puts the trader at a probably significant drawdown.
Let us look at the overall probability to win or lose in this scenario. From the 7891 random runs, only 390 were able to reach the 10x of initial capital target, while 7501 went completely bust. Due to the risk level used there are no intermediate scenarios between achieving the target or going broker (as the negative bias and risk ensure that if you haven’t achieved the target you go broke by the end of the test). The probability to win is actually 4.94%, this is dramatically less than the around 9.5% needed to break even. The difference is clearly due to the spread, which causes a very negative bias at high risk levels that ensures that the number of successful traders is about half of those that would break-even with losers. A trader seeking a high profit through high risk, subject to the intrinsic randomness of the market is therefore at a dramatic disadvantage, since the negative bias is huge and causes the random walk to converge rapidly towards a very negative scenario. Interestingly enough, the above shows about a 95% of wipe-out cases vs a 5% survival rate. Could this be the source of the all-so-common 95% of traders lose money saying among retail traders? Just a thought.
–
–
From the above you could picture that the around 5% of traders who make it would believe that they have some sort of “market secret” since they were able to increase their capital by 10x within a timeframe that is tremendously small by all investment standards (just a year or two) with average drawdown period lengths that are very small (100-150 days). Similarly you can picture 5% of those traders achieving 100x (0.25% of overall traders) and 5% of those traders achieving a 1000x increase (0.01% of overall traders). These traders would be bound to become legends but their feats would be impossible to reproduce systematically (since they are the consequence of random chance). Since there are at least a few hundred thousand retail Forex traders, you can expect at least a few across a 10 year period to turn 100 USD into 100,000 USD, just by pure chance. This shows you that a track record with a 1000x increase does not mean that a trader has an edge, it can still be the result of pure random chance, although improbable, possible. However consider that if a setup has a chance of coming from randomness below 0.1%, most people would be comfortable with trading it, how stringent must you be to avoid being fooled by randomness?
If you would like to learn more about system building and how you too can use techniques such as data-mining while properly accounting for biases please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading in general . I hope you enjoyed this article ! :o)







I can only laugh Daniel, this is brilliant! Thanks for the excellent article