When solving problems using machine learning there is typically a relationship between errors within training sets, errors within testing sets and model complexity. This relationship and the arrival at an optimum trade off between model variance and bias is commonly denoted the bias-variance trade off. Today we are going to talk about the bias-variance tradeoff in trading and why it is a much more complex problem than in other deterministic machine learning problems. Furthermore we are going to talk about the irreducible error, an error component that is usually small or not present in many modeling problems and that poses the most fundamentally important error source when building trading strategies. Note that I used some images from this post which contains a very good explanation of the bias/variance tradeoff.
–
–
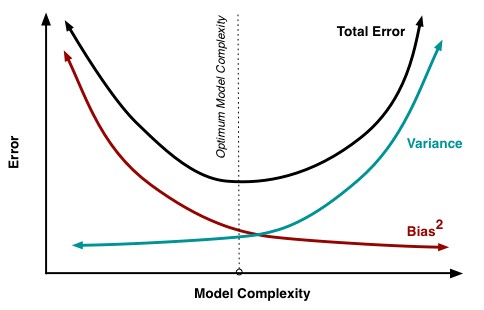
When you build a model to describe some behavior – for example a model to predict the movies a person might like – you can usually see that the error of your predictions within your training set is reduced as model complexity increases. A 10th degree polynomial will usually have much less error in the training set than a linear model and so on. This is a simple consequence of the degrees of freedom within the model that allow a much better adjustment to the data at hand. However this adjustment – or fitting – usually means that results improve up to a point on unseen data but after that point the error increases in the testing set. This means that bias decreases with model complexity up to a point – your predictions in unseen data become better – and then variance starts increasing as you gain improvement in training but not in testing data.
The above is the reason why curve-fitting bias is often considered an important source of system failure in algorithmic trading. If a model worked in a back-test and failed within real data testing then it is easy to assume that – as in most other model building efforts – the problem is that you did not arrive at a proper bias-variance trade off and you created something that was too complex for the amount of data that you had at hand. In traditional model building this means that you should either reduce your model complexity or use more data so that your model can behave properly under unseen data. This in fact works to reduce curve-fitting bias in trading as larger data for “training” – in this case meaning any generic model building effort – should in all cases lead to less curve-fitting bias and lower complexity should help – up to a point – if the model is very complicated.
–
–
That said, the fact of the matter is that model-building related sources of bias, like curve-fitting bias and data-mining bias, are not the only sources of error that generate failure in trading strategies. There is another fun error class which is called irreducible error which points to a source of error that is brought by the stochastic nature of the problem being solved and the lack of enough data to properly describe the problem. It is the valley in the bias-variance trade off graph, the minimum error you could get to. In the trading case this is an error related with the market simply changing to something else that cannot be reduced because of the unpredictable nature of these changes. No matter how much you attempt to reduce curve-fitting and data-mining bias, irreducible errors will always be present and they cannot be reduced — as the name implies.
The above is the consequence of trying to solve any problem where all possible data is not available and therefore where the problem’s description can change significantly as a function of time. Any model you build will have to lose its edge at some point – a phenomenon often called “alpha decay” in stock trading – as irreducible errors will eventually take their toll. This applies also to models that adapt, or that adapt to adapt, or that adapt to adapt to adapt and so on, as all of these adaptation mechanisms are always calibrated on already seen changes – historical data – and the irreducible error component implies the generation of errors that you cannot adjust for. If you could reduce the error, then it wouldn’t be irreducible. Irreducible errors come from using limited data for model building since we don’t have access to infinite market data.
–

–
What can you do then? Although irreducible error exists they are not the same across every market and every instrument. When building strategies you should be able to calculate the alpha decay of your systems and build strategies within symbols where the alpha decay has been the lowest. Even if there is nothing you can do to reduce irreducible errors there are certainly things you can do to ensure that you trade where the irreducible errors are the smallest in magnitude (or at least have been the smallest in magnitude up until now). If you would like to learn more about model building and how you too can trade portfolios using thousands of strategies please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading strategies.




