During the past several years I have coded a variety of different neural network systems for FX trading using a significant number of different input/output structures and network topologies. However one of the things that all my approaches have had in common is the use of either pure price return series or the close/open series as inputs. On today’s post I want to go a bit beyond this initial template to show you how we can also obtain good performing trading systems using more elaborate price calculations as inputs. Although the results of this exercise are not significantly better trading systems than what can be found using simpler inputs the results are indeed different and provide a venue for the diversification of already available machine learning strategies. This post will focus on how I used the Relative Strength Index (RSI) for the creation of such strategies.
–
double NN_Prediction_i_simpleReturn_o_tradeOutcome(int learningPeriod, int barsUsed, int tradingHour, int BE, double initial_SL, int frontier, double minStop, int dsl_type, int trainingEpochs)
{
//get problem data
RegressionDataset dataset = regression_i_simpleReturn_o_tradeOutcome(learningPeriod, barsUsed, tradingHour, BE, initial_SL, frontier, minStop, dsl_type);
FFNet<FastSigmoidNeuron,FastSigmoidNeuron> network;
unsigned numInput=barsUsed;
unsigned numHidden=(int)((barsUsed+2)/2);
unsigned numOutput=2;
unsigned numberOfSteps=trainingEpochs;
unsigned step;
network.setStructure(numInput, numHidden, numOutput);
initRandomUniform(network,-0.5,0.5);
SquaredLoss<> loss;
ErrorFunction error(dataset, &network,&loss);
RpropMinus optimizer;
optimizer.init(error);
for(step = 0; step < numberOfSteps; ++step){
optimizer.step(error);
}
network.setParameterVector(optimizer.solution().point); // set weights to weights found by learning
Data<RealVector> testOutput;
RegressionDataset datasetInput = p_regression_i_simpleReturn(barsUsed);
testOutput = network(datasetInput.inputs());
if (testOutput.element(0)[0] > 0 && testOutput.element(0)[1] < 0) return(1);
if (testOutput.element(0)[1] > 0 && testOutput.element(0)[0] < 0) return(-1);
return(0);
}
–
When creating a neural network trading strategy I have always advocated for the creation of algorithms that are constantly retrained on each bar using a moving window (therefore avoiding common pitfalls encountered by academics) and which have output structures that are predictive of actual profitability rather than simply directionality or volatility. Lately at Asirikuy we have successfully implemented an approach using simple returns as inputs as the outcome of long/short trades as outputs. This approach builds examples where we want to draw a relationship between the simple returns of the price series and the actual outcome of a trade that is managed through a given trailing stop mechanism (we presently implement 5 different choices for trade management). Since this approach is successful at generating systems I then wondered whether the inputs could be changed to obtain substantially better or at least equally profitable but uncorrelated trading results.
In the past my efforts to build indicator based neural network systems had always been quite unsuccessful. I had tried several different indicators including moving averages, bollinger bands, stochastics, etc but had never been able to find a suitable replacement for price returns. I had always been particularly convinced about the relationship between the RSI and future price returns – at least on the EUR/USD – as several simple systems I had coded in the past (including the now old and freely available Atinalla FE) were at least partly based on this indicator. With this in mind I decided to give it a shot using our Shark implemented Neural Network algorithm (above) and the output structure that we have successfully used to create our current ML repository (which today has more than 80 trading systems based entirely on uncorrelated continuously retraining ML mechanisms).
–
//code modifications in the regression_i_simpleReturn_o_tradeOutcome function
Data<RealVector> inputs(period,RealVector(barsUsed*2));
...
for(j=0;j<barsUsed;j++){
inputs.element(m)[2*j] = iRSI(0,5,tl+j+i+1)/100;
inputs.element(m)[2*j+1] = iRSI(0,10,tl+j+i+1)/100;
}
//code modifications in the p_regression_i_simpleReturn function
Data<RealVector> inputs(1,RealVector(barsUsed*2));
...
for (j=0;j<barsUsed;j++){
inputs.element(0)[2*j] = iRSI(0,5,j+1)/100;
inputs.element(0)[2*j+1] = iRSI(0,10,j+1)/100;
}
–
I finally decided to use two different RSI periods 5/10 for the past 2 bars as inputs, giving a total of 4 input values. The system trades on each day at 5 GMT +1/+2 and on this hour builds 105 examples using this input/output structure to train a neural network using sigmoid functions. For the outputs I used the outcome of long/short trades (meaning two neurons) that used a trailing stop mechanism where the stop is moved on each new bar open to 1.4 times the ATR from the open if the new stop value is more favorable than the current one. The NN has a topology of 4/2/2 where this represents 4 input neurons, 2 hidden neurons and 2 output neurons; this algorithm is retrained on every bar (300 epochs) when trading happens using a moving window of 105 examples. Above you can also see a small section of the code showing how I generated the RSI inputs on the regression_i_simpleReturn_o_tradeOutcome function in the F4 framework.
–
–
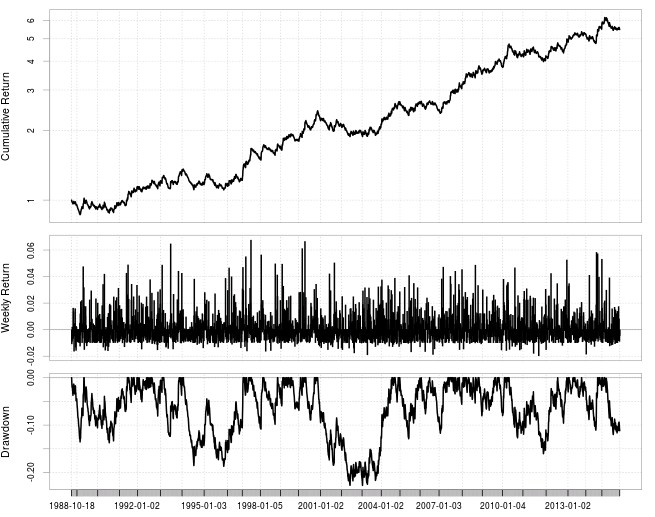
My first results with the above experiment have been quite satisfactory with the generation of trading systems with similar profitability than when using simple returns on the EUR/USD. However these systems have low correlation with strategies created using simple returns, showing that the predictive ability is potentially complimentary to that of Neural Network strategies based on these inputs. Compounded results look highly linear on a logarithmic y axis (see performance graph above) and maximum drawdown values are around 20% with a 1% risk per trade on a back-test spanning the past 27 years. Contrary to some other results there is no significant declining of the graphs slope during current years, suggesting that this technique is successfully able to tackle current market conditions.
I also still haven’t explored the variation of the RSI periods or the results on other pairs, reason why these indicator results might still be quite below what can be achieved using this type of inputs. Nonetheless the results are encouraging as they suggest that the current output structure used can also work with inputs that are different from the typical price return inputs. With this in mind I hope to create more diversified strategies for the Asirikuy community and hopefully find even better results on symbols where price returns offer only poor predictive ability. I will continue posting about these systems as my research in this field advances.
If you would like to learn more about machine learning and how you too can create your own constantly retraining machine learning strategies please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading.