Financial times series are often described as being a mixture of both random and deterministic elements. As traders we seek to profit from the deterministic elements of the time series while the stochastic elements make the time series inherently harder to predict. Since there are a myriad of financial instruments to trade in the Forex market, it makes sense that we should choose those instruments for which the deterministic element is more prevalent (the least random series) so that we can get more successful trading results. On today’s post I will be talking about using approximate entropy as a way to monitor the FX market, specifically I will be showing you how you can measure entropy of recent time series quite easily using R and how this can help you choose which pairs to trade.
–
library(ggplot2)
library(quantmod)
library(pracma)
allSymbolEntropies <- data.frame(matrix(NA, nrow = 17 , ncol = 2))
colnames(allSymbolEntropies) <- c("symbol","entropy")
getSymbols("EUR/USD",src="oanda")
fxdata <- EURUSD
allSymbolEntropies$entropy[1] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("AUD/USD",src="oanda")
fxdata <- AUDUSD
allSymbolEntropies$entropy[2] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("NZD/USD",src="oanda")
fxdata <- NZDUSD
allSymbolEntropies$entropy[3] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("GBP/USD",src="oanda")
fxdata <- GBPUSD
allSymbolEntropies$entropy[4] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("EUR/JPY",src="oanda")
fxdata <- EURJPY
allSymbolEntropies$entropy[5] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("GBP/JPY",src="oanda")
fxdata <- GBPJPY
allSymbolEntropies$entropy[6] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("USD/JPY",src="oanda")
fxdata <- USDJPY
allSymbolEntropies$entropy[7] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("USD/CAD",src="oanda")
fxdata <- USDCAD
allSymbolEntropies$entropy[8] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("EUR/CAD",src="oanda")
fxdata <- EURCAD
allSymbolEntropies$entropy[9] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("USD/CHF",src="oanda")
fxdata <- USDCHF
allSymbolEntropies$entropy[10] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("EUR/AUD",src="oanda")
fxdata <- EURAUD
allSymbolEntropies$entropy[11] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("AUD/CHF",src="oanda")
fxdata <- AUDCHF
allSymbolEntropies$entropy[12] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("AUD/CAD",src="oanda")
fxdata <- AUDCAD
allSymbolEntropies$entropy[13] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("GBP/AUD",src="oanda")
fxdata <- GBPAUD
allSymbolEntropies$entropy[14] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("CHF/JPY",src="oanda")
fxdata <- CHFJPY
allSymbolEntropies$entropy[15] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("CAD/JPY",src="oanda")
fxdata <- CADJPY
allSymbolEntropies$entropy[16] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
getSymbols("EUR/CHF",src="oanda")
fxdata <- EURCHF
allSymbolEntropies$entropy[17] <- approx_entropy(fxdata,
edim = 2, r = 0.2*sd(fxdata), elag = 1)
allSymbolEntropies$symbol <- c("EURUSD","AUDUSD","NZDUSD","GBPUSD","EURJPY",
"GBPJPY","USDJPY","USDCAD","EURCAD","USDCHF","EURAUD","AUDCHF",
"AUDCAD","GBPAUD","CHFJPY","CADJPY","EURCHF")
allSymbolEntropies <- allSymbolEntropies[order(allSymbolEntropies$entropy),]
allSymbolEntropies$symbol <- factor(allSymbolEntropies$symbol,
levels = allSymbolEntropies$symbol, ordered = TRUE)
ggplot(data=allSymbolEntropies, aes(x=symbol,y=entropy)) +
geom_bar(fill="blue", width=.8, stat="identity") +
guides(fill=FALSE) +
xlab("Pair") + ylab("Entropy") +
ggtitle("Entropy values")+
theme(axis.text.x = element_text(angle = 90, hjust = 1))
–
Let’s first understand a bit more what approximate entropy is about. When you have a time series you have a sequence of elements that can be organized either randomly or in certain patterns. Two time series can have the exact same standard deviation, variance, mean and other descriptive statistic measurements, but one can show repetitive patterns while the other can be completely stochastic. Traditional descriptive statistics cannot distinguish between both – as from this perspective they are the same – therefore we need a more elaborate measurement to try to tell which one is more random than the other. The wikipedia page on approximate entropy gives a good example and goes deeper into the mathematical nature of the measurement.
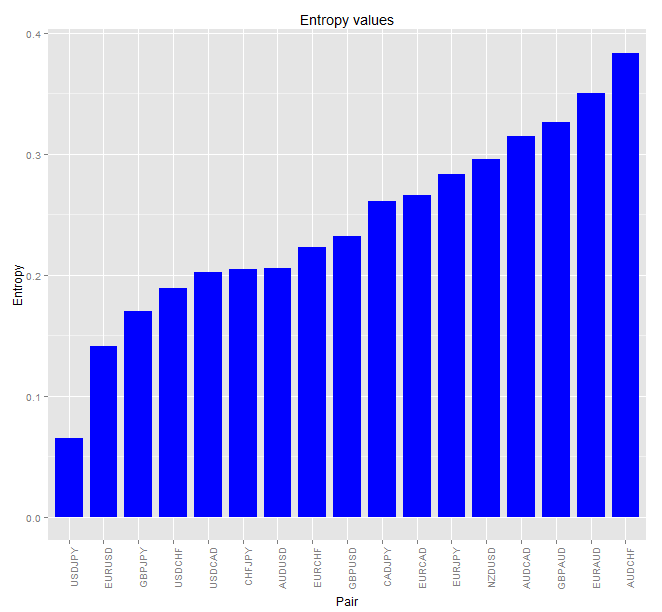
We can easily perform a measurement of approximate entropy in R using the “pracma” package with data obtained from Oanda using the quantmod package. In this manner it is easy to obtain entropy measurements for the past 500 days of data, allowing us to draw a picture of the current state of the FX market from an entropy point of view. The code above shows you how this can be done. The code also generates a graph using gpplot2 that shows you the entropy measurements going from lowest to highest (graph below). With this script you can easily obtain and compare entropy values for 17 symbols. You can add/remove any symbols if you wish, by simply adjusting the indexes and dataframe size.
–
 –
–
Once you have entropy measurements we now have to ask ourselves how this helps us choose which pairs to trade. Pairs with the lowest entropy values are the ones that have the highest non-random components, while pairs that have the highest entropy values have the highest random components. I prefer to also multiply the entropy values by the trading cost of each pair (in pips) so that I can get values that are also adjusted against trading costs. Patterns might be more readily available on a more expensive pair, which means that the advantage may be completely nullified against a cheaper pair with a lower advantage. From this graph it seems clear that we should be trading either USDJPY, EURUSD, GBPJPY or USDCHF while a pair like the AUDCHF would seem to be the least favorable to trade.
It is also worth wondering whether these values change significantly across time or whether they are quite constant. I repeated the above analysis using 25 years of data for the 4 majors and the results show that the qualitative order remains fairly similar although on a longer term perspective the USDCHF becomes the pair with the lowest entropy. The increase in entropy for the USDCHF under recent times may be in a big part due to the introduction of the EURCHF peg in 2011, which might have increased the amount of randomness for this pair. Note however than long term entropies are generally lower overall.
–
–
It therefore seems most favorable to trade pairs for which the long term and short term entropy values are low. This means that we have pairs for which there is a certain stability regarding the amount of deterministic/random components, definitely having a long term value that is of similar magnitude when compared with the short term value is also advantageous. Entropy measurements could also provide a way to trigger/stop trading on certain symbols as entropy increases imply that the time series is becoming more random and therefore trading is becoming more difficult. Graphing entropy Vs time provides you with a cool way to measure this.
Although entropy is not the only consideration when choosing a pair to trade (other things such as random walk hypothesis tests, costs and liquidity should all be considered) it is a very useful measurement to aid you in your decision to trade or not trade a given instrument. If you would like to learn more about symbol analysis and how you too can generate automated systems to trade any chosen pair please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading in general.






Interesting starting post. Can you give an example of a trading system that might use some rolling entropy computation as a filter or whatnot? Furthermore, is this a computation that’s computed in a rolling manner, such as an SMA200, or would one have to specifically do a rollapply to get a consistent stream?
One possible idea just off the top of my head is to use it as a universe-filtering tool, looking at the computation every month with a rolling 4-month time frame, for instance, ala Flexible Asset Allocation.
In any case, I’m hoping you’ll follow up on this and do some more in-depth demonstrations.
-Ilya (quantStratTradeR)
Nice post, thanks.
It would also be interesting to see the results from varying the observation interval in intraday data.
One obvious enhancement to the R script (to save on copy and paste) would be to iterate through the instrument set in a for() loop, eg:
symbol.set = c(“EURUSD”,”AUDUSD”,”NZDUSD”,”GBPUSD”,”EURJPY”,”GBPJPY”,”USDJPY”,”USDCAD”,”EURCAD”,”USDCHF”,”EURAUD”,”AUDCHF”,”AUDCAD”,”GBPAUD”,”CHFJPY”,”CADJPY”,”EURCHF”)
allSymbolEntropies <- data.frame(matrix(NA, nrow = length(symbol.set) , ncol = 2))
colnames(allSymbolEntropies) <- c("symbol","entropy")
for (x in 1 : length(symbol.set)) {
s = paste(substring(symbol.set[x],1,3), substring(symbol.set[x],4,6), sep='/')
cat("downloading", s , '\n')
fxdata = getSymbols(s, src="oanda", auto.assign = F)
allSymbolEntropies$entropy[x] = approx_entropy(fxdata, edim = 2, r = 0.2*sd(fxdata), elag = 1)
}
allSymbolEntropies$symbol = symbol.set