We have all heard about some classic problems that are inherent to the process of inductive learning. Among these the most prominent is usually over-fitting, where a generated model tends to fit the training data extremely well and then lacks the ability to provide suitable generalizations. However beyond the increase in bias that usually comes from over-fitting there are some additional problems that can be generated depending on the model at hand. On today’s post I am going to discuss some of the signs of over-fitting – some of which you might ignore if you’re not careful – plus some of the problems that are generated from over-fitting that tend to hide behind some of the randomness inherent to the mechanisms used to create some models.
–
–
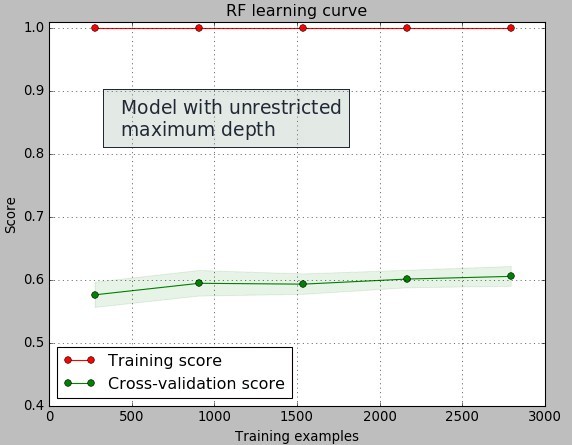
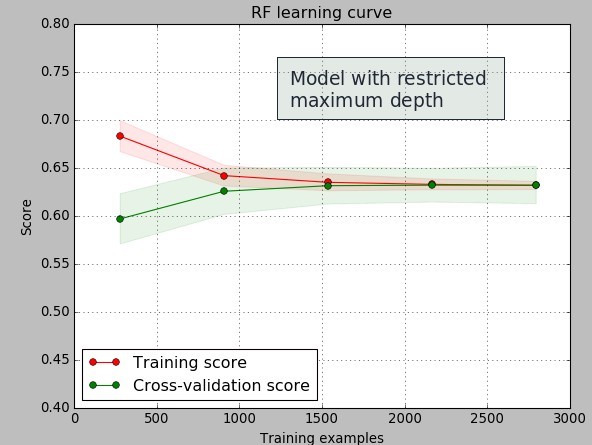
In inductive learning you never want to take the training data too seriously. Since your data is usually a sub-set of a much larger population taking induction too far will usually lead to results that describe the training data too well but then fail to represent the behavior of the general population. In the example showed above I have created a random forest classification model for the prediction of whether a system will or will not profit for the 6 months following its creation from historical data. The pictures above show the learning curves for the models created using random forests with and without maximum depth restrictions.
From these images it is easy to see over-fitting. When the maximum tree depth is unrestricted we see that the created models perfectly describe the training data – the error is practically zero as everything in the training set is classified properly – while in the testing set the classification error is much higher. We refer to this as a high variance since we have a very large difference between what we get in the training set and what we obtain from the testing set. When the maximum depth is restricted we can see that the training errors come much closer to the testing errors – we get very little variance when the amount of examples grows above 1500.
–
–
That said the overall testing error of the models is similar – although clearly better in the restricted depth case – so we might be tempted to think that they classify almost the same way even though we can see over-fitting when we have unrestricted tree depths. There are even some cases where you’ll see the testing error being lower in the testing set when you have unrestricted tree depths even though the difference between training and testing errors is very large. You might be very tempted to take the model that seems to be more curve-fitted, even at the very high variance it seems to offer, just because it appears to offer you similar or even better classification errors.
The problem here is how random forests are created. Models that are over-fit in random forests not only tend to have high variance in terms of the difference between training and testing set scores but they also present a problem related with model convergence. When the model is not curve-fitted as in the second case, increasing the number of estimators generally causes the model to reach a convergent conclusion – the model variance tends to reduce as the number of estimators increases – while in the case of a curve-fitted solution the number of estimators tends to follow something alike a random walk, where you never seem to reach a case of model convergence. When the model is not curve fitted if you have enough estimators you can generate the model 10 times and get very similar results, when the model is heavily over-fit this is not the case.
–

–
Whenever I created random forest models that were highly over-fit I could never get predictions that were consistent and that became less variable as the number of estimators increased but what I got what simply a model that every time I generated gave a different answer. This is a consequence of the great number of degrees of freedom that you gain when you allow for such a large level of complexity. In this cases reaching convergence of the model would possibly take tens of thousands of estimators while in the case of the models that are not over-fit this can be achieved with little over 150 trees. purchase Seroquel amex online without prescription Variance as a function of the number of estimators needs to become smaller and converge to a relatively small value when you use random forests, otherwise – regardless of what you might get in individual cross-validation tests – the model is probably not going to be useful.
If you would like to learn more about machine learning and how you too can use machine learning algorithms to make predictions about trading strategies or even create systems that use constantly retraining machine learning models please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading.strategies.




