Monte Carlo simulations are – without a doubt – one of our most useful tools when building and testing automated trading strategies to trade the markets. There are many ways in which this type of simulations can be used although they are most commonly exploited for the determination of “worst cases” of mechanical trading strategies. During the past few weeks – while running Monte Carlo simulations for some Asirikuy portfolios – I found a very interesting phenomena related to inherent system quality and the abundance of back-testing draw downs within distribution based Monte Carlo simulations. After doing some analysis it became apparent that such measurements are an interesting measure of system quality which can be specifically used to assess a system’s like hood of robustness.
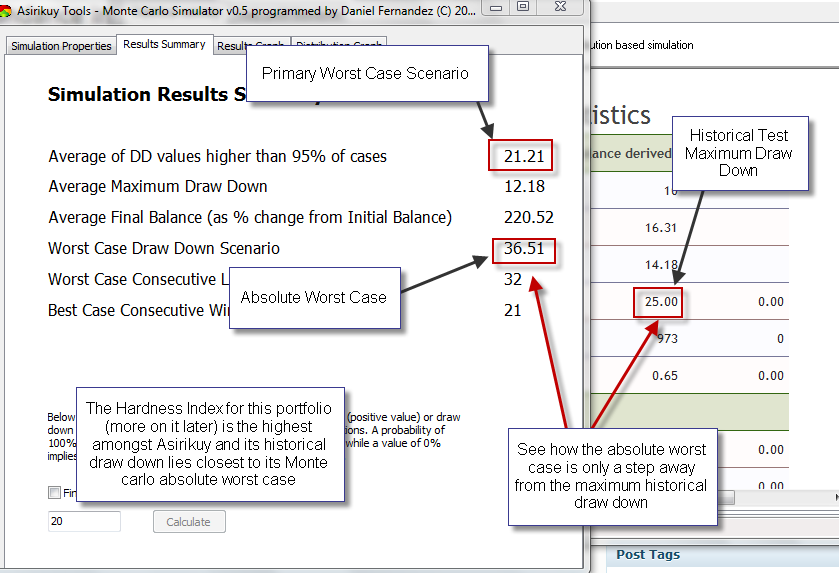
In Asirikuy we generally determine two important values through 100K iteration Monte Carlo simulations. The first one of these values is the average of draw down values which constitute the worst 5% of all studied cases and the second one is the overall worst case scenario seen through the whole iteration specter. The first value varies little between successive runs while the second one can vary significantly as it sometimes constitutes very odd and unlikely statistical anomalies which tend to fail to converge on certain cases. This is the reason why we use the first one as a primary worst case threshold with the second one being the absolute proof of system failure (if a system achieves the worst case of a Monte Carlo run then it is definitely not following its long term statistical characteristics). Generally we will not trade systems down to the Monte Carlo worst case draw down since the 5% worst case average provides a good way to stop trading systems at a reasonable confidence interval.
–
Recently however I run into a very curious thing which I hadn’t seen before. Certain portfolios give Monte carlo simulations whose primary worst case target (average of worst 5%) falls above the maximum historical draw down. This means that the draw down within the simulated period was a significantly bad case of the particular trading distribution, meaning that future draw downs will most likely not fall below the historically attained values and, if they do, then probably the reasonable limit to use would be the Monte Carlo absolute worst case instead of the regular average used for systems when this is not the case.
The interesting thing now is to analyze which systems give these results and what this is telling us about the behavior of these particular systems. Up until now I have only been able to find this occurrence on a few portfolios which trade either a large array of instruments with very robust systems or on systems which trade during extremely long periods of time (like our 20 year Coatl portfolio). This led me to believe that this phenomena has something to do with system robustness. Not surprisingly, the Monte Carlo absolute worst case scenario is also less than twice the historical maximum draw down, meaning that even if we consider this as the real worst case for such portfolios it does not constitute a dramatic shift towards higher risk tolerance.
The interesting thing here is that the historical performance draw down seems to already be close to what we would consider the worst statistical cases of those particular distributions, meaning that the system has already hit “rock bottom” within the simulations, within the limits of the distribution. This means that what you see within the simulations in most probably in line with what you will get in the future, a measure of robustness. This is in fact something rare to find as most systems and portfolios will have primary worst cases of about twice their historical maximum draw down and absolute worst cases of even 4 to 5 times this value.
Based on the type of systems that reach this scenario and the above analysis, it seems interesting to note that the abundance of the historical draw down level within Monte Carlo simulations tends to give a good idea of overall system robustness. A system which has reached a historical maximum draw down level which falls within a very low probability within its Monte Carlo simulation is actually very likely robust since its worst case scenario will be close to its maximum draw down and therefore future performance – if the system continues to work – will match closely historically obtained results (since they are already close to rock-bottom).
It is also important to see that this does NOT imply that worse portfolios are more robust as doing the above does not simply imply the reaching of a deeper draw down within the backtest as a draw down behavior which makes the distribution “worse” will also cause the Monte Carlo worst case targets go lower and therefore will cause a “chasing” of low draw down abundance. The interesting aspect of the above portfolios is that they reach low draw down abundance without making their distributions any worse and therefore the historical tests constitute a very realistic picture of how the system behaves under even the most unfavorable conditions.
This way of looking at Monte Carlo simulations gives us a clear numerical criteria which we can use to judge system robustness that does not depend on some complicated numerical calculations which make many assumptions about what makes a system or portfolio robust (like the hardness index). Nonetheless it is important to recognize that hardness index values and draw down abundance are in fact very heavily correlated (Ill leave this data for a future post), giving us yet another hint that the abundance of the historical maximum draw down within Monte Carlo simulations is a clear measure of system robustness.
If you would like to learn more about Monte Carlo simulations and how they can be used to analyze system worst case scenarios please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading in general . I hope you enjoyed this article ! :o)