Using the largest possible amount of data when back-testing to generate systems that can better accommodate more market conditions is a fairly intuitive and well rooted idea in algorithmic trading. However there seems to be a general lack of quantitative evidence to say whether this is actually the case or if there is an optimum amount of previous market conditions to use that may provide a higher probability of success for out of sample (OS) trading. Since determining how much data to use for the creation of trading strategies is fundamental to the design of a trading methodology, I have decided to run some experiments in order to find out what the best amount of historical data to use for system generation actually is. Through the rest of this post I will show you some of the quantitative evidence I have obtained through my research as well as some of the conclusions I have been able to reach through this analysis.
So how do we find out what the historically optimum in-sample size for system creation has been? The first step is to generate a large amount of profitable and symmetric in-sample systems using different sizes for the in-sample period and then compare their success rate across a fixed out of sample period size. It is also important to distribute this in-sample/out-of-sample pairs randomly across the whole back-testing data in order to avoid the fitting of the results to some particular set of market conditions. For example in order to evaluate the success rate of a 500 day in-sample period I generate 1000 profitable and symmetric systems using randomly selected 500 in sample periods followed by a 365 day out of sample. One test might be from 1992 to 1994 with an out of sample from 1994 to 1995 while another might be from 2005-2007 and then the out of sample from 2007 to 2008. I performed this analysis using in-sample sizes from 100 to 6500 days with a constant out of sample of 365 days. I also performed this analysis on EUR/USD data from 1986 to 2012 (before 2000 using DEM/USD data).
–
–
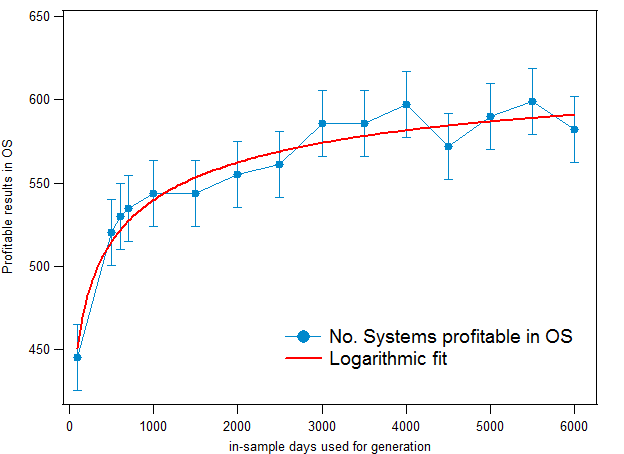
The first result we can analyse from the above experiment is the difference between the number of profitable and unprofitable OS periods. Intuitively we would think that the number of systems profitable in the OS would increase as a function of the in-sample size, since more market conditions would allow us to better accommodate the results of the OS period. This happens to a certain extent but it is also true that after a given point the increase of the in-sample size does not lead to a significantly better edge. As you can see in the image above, the number of systems profitable in the OS increases logarithmically as a function of the in-sample see (logarithmic fit in red), this predicts that the increase in your edge as the in-sample size increases will be less significant as your in-sample becomes larger and larger. This hints that the number of market conditions might be convergent to a certain extent, meaning that after a certain point you cannot “better adjust” to new market conditions based on past ones because you have already taken into account all the behaviour which is relevant. Note that the error lines show the variability I experienced after doing 10 different runs to account for the random nature of the system generation procedure used by Kantu.
These results also show us that there is a minimum number of in-sample days which is required to reach acceptable results. Systems created using data from less than 500 days are especially unreliable (out of sample edge is almost completely lost) while systems created with more than 3000 days of in-sample data tend to reach similar results. This shows us that there is a bare minimum of information that is needed to gain an edge in the OS while introducing much larger amounts of data only improves this edge slightly. In general this also supports the fact that 3000 days (about 8 years) is the best starting point for system generation. Using more years can give you a further advantage but it doesn’t seem to be fundamental for success in the OS. This supports our development methodology at Asirikuy, where we have used 9 year periods for system generation and optimization. From this it also seems important to note that there is in fact an improvement of the OS success with the in-sample size so using the largest possible in-sample size you can will confer you an additional advantage – at least in the case of the EUR/USD – even if this is not too great.
–
–
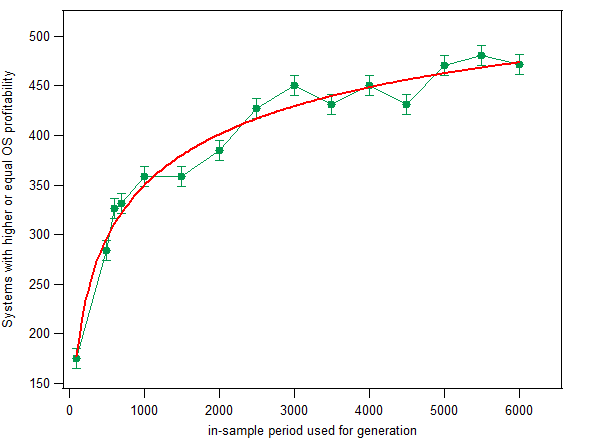
Another interesting thing to analyse is how the OS profitability varies according to the size of the in-sample period. Obviously we want to have OS periods that are just as or more profitable than the in-sample (measured as (absolute profit)/(total trades)) so that we can have a smaller probability of being disappointed by our OS performance. The graph above shows you the number of systems with OS profitability higher or equal than the in-sample per trade profitability. As you can see the results are fairly similar to the initial results we discussed – where we analysed only the net number of OS profitable systems – showing that the probability to have a profitability higher than the one of the in-sample period is also logarithmic in nature. The probability to have a better OS period – from a profitability perspective – also increase with the size of the in-sample period, the probability increases very fast at first, then increasing more linearly as we reach larger in-sample sizes. In contrast with the previous case, the increase of probability here is far more pronounced, hinting that – although the number of systems profitable in the OS might not increase very much with larger in-sample sizes – the increase in the probability of having a more profitable OS period – relative to the in-sample – is higher.
It seems that the above quantitative evidence supports the design paradigm that suggests the inclusion of as much data as possible in the system generation process. Having more data seems to lead to a higher probability of out of sample success, both from a probability of net profit and a probability to have profits higher than those of the in-sample period. Therefore it would be advisable to always include as much data as possible when generating a strategy because this generates an additional probability to be successful under unseen market conditions. However it is also worth pointing out that the nature of both studied behaviours is logarithmic, meaning that we should expect convergence of these values towards some tangent as the in-sample size grows much larger. From the derived logarithmic fits it seems to be that in-sample sizes above 8000 days would give practically no improvement in the expected OS performance.
However the are still a lot of questions to answer about the above. Is this process the same across other pairs? Is this process the same across other markets? How does the out-of-sample size affect these results? These are all very interesting questions that I will certainly continue to research within the next few months :o). If you would like to learn more about system generation and how you too can perform your own research please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading in general . I hope you enjoyed this article ! :o)





Hello Daniel,
thanks for your interesting article. I really like the level of insight you provide about the algorithmic trading, here, as well as in the Asirikuy community. I am impressed by the power of Kantu (which I’m already using, by the way) and I find it a great tool to improve my understanding.
Concerning the todays article, I wonder about the size of the OoS you chose: 365 days is a very comparable to a DD length of a respectable long term profitable system. Don’t you think that this factor can alter the conclusions you have drawn here? *Ideally*, I would have evaluated an OoS period of n times a representative DD length of every system. What do you think?
Thanks again!
Lorenzo
Hi Lorenzo,
Thank you for your post and kind words about my work :o) Sure, you are absolutely right about the Max DD length and this is why I chose this OS period length on purpose. My idea was that if there was a predisposition of systems to go into drawdown periods soon after the in-sample period then an OS length that wasn’t so long would show systems that weren’t fit to new market conditions as losers pretty quickly. I also wanted to choose an OS length that wasn’t so long because in practice most people are bound to evaluate methodologies that approach trading from a yearly perspective (purely psychological I believe). Changing the out of sample length is indeed very interesting but I can give you a little heads up in that it doesn’t affect the conclusions reached in this article (if you choose an OS of 2000 days you will reach very similar plots). However there are very interesting conclusions about the OS length and there is indeed an optimum OS (unlike the in-sample length which seems to be “the more the better”). My next step is to build a 3D map of the OS and in-sample length so that we can gain a deeper insight. Thanks again for posting Lorenzo :o)
Best Regards,
Daniel
You first say:
“Intuitively we would think that the number of systems profitable in the OS would increase as a function of the in-sample size, since more market conditions would allow us to better accommodate the results of the OS period.”
and then you say
“This happens to a certain extent but it is also true that after a given point the increase of the in-sample size does not lead to a significantly better edge.”
Obviously, you imply that edge is related to the number of profitable systems in the OS. However, you have not demonstrated the assumed link. If that link were true, every trader with a backtesting engine like MT would be rich trading a portfolio of systems that pass OS testing. Reality tell us that 99.999999% of OS performance is random. In this respect your results lack significance in a gross way. It is a study that virtually tell us nothing because of the lack of a measure of significance of OS results. You just dealt with the numbers of OS results but not with their significance and any edge they offer.
To be honest I was really surprised by this. I din’t expect this from you because you came across as knowledgeable on this subject. But it appears that your approach is quite basic and quite rudimentary I’m afraid to say. I hope you are open to criticism. It is through criticism that we can all become better.
Hi Rick,
Thank you for your comment :o) Hey I am always open to criticism! I think that the problem comes from the fact that I didn’t explain myself well enough within the post (obviously my bad). Let me now make some clarifications:
1. The initial part of the study just measures the number of systems profitable in the OS out of 1K systems generated across randomly chosen in/out of sample couples where the OS part is always 365 days long and the IS (in-sample) part is varied. This just means that there are more OS profitable results but it tells us nothing about whether having more systems profitable in the OS offers any edge (I agree here as we could simply have huge losers that take out even a larger number of systems profitable in the OS).
2. The second part of the study goes a little bit deeper – the second graph – and examines the number of systems that generated results in the out of sample that exceeded the per-trade profitability in the in-sample period. This shows that as the in-sample size increases so does this number. This shows us that the probability to have results that exceed the in-sample trading becomes larger.
3. A part that I didn’t publish here – which perhaps is what you’re missing – is that the sum of all OS results (profitable and losing ones) is always positive and becomes more positive as the IS size grows larger. This unequivocally demonstrates that the system generation process gives a larger OS edge as the in-sample size grows bigger.
4. What do you mean by “passing OS testing” ? What you are assuming here is that the selection process to trade live happens after the OS period evaluation. I am not supposing here that a trader will be able to select a generated system based on OS performance as it is usually done (like generate a system from 2000-2010 then only trade live if its profitable from 2010 to 2012 or something along these lines), what I am trying to evaluate here is what would have happened if the systems had been traded based simply on their IS performance. Suppose a trader had generated 1K systems (as I have) and had then traded all of them live during the next year (just as an example), the result would have been a net positive forward performance that would have increased depending on the trader’s IS size. This means that if right now you want to generate a parameterless price action based system to trade the daily EUR/USD, it is a rational assumption to suppose that using the largest possible IS size and trading 1K systems will allow you to come out profitably after 1 year (the OS size in the test). The catch here is that you cannot trade 1K systems, more on this in the following paragraphs.
5. Certainly this doesn’t mean that a trader with MT4 and a back-tester can easily trade profitably because the above performance converges when the set is very large. Even on the best case the chance of having a positive performance in the OS (forward period) is only 58.2% across 1K systems. If you do a Monte Carlo simulation you will see that a trader who produces just 10 systems will have a very good chance of coming out with losses since the chance of having an unprofitable outcome is still too large. Yes, if you traded a large amount of systems generated as the above method suggests you are bound to be profitable going forward but this isn’t actually possible because in practice you can only trade a small number of strategies. The next step for someone who want to be profitable is to develop a selection criteria so that profitable trading can happen reliably on a selection of a small number of generated strategies (and this is no easy task because you must also take into account the probability of the sum of system performance being positive).
I hope this clears it up Rick :o) I am sorry if the posts sometimes miss data but you are always welcome to ask if you have any questions about this or something you think should be added. I also never want to imply that anyone can easily get rich by using any of the information or tools I device. I am just studying certain aspects that relate IS and OS performance, attempting to draw some light into how large sets of generated strategies show behaviour that seems coherent. I am also not using OS as part of the analysis but I see OS as periods where I would actually be trading the systems live, with the idea to eventually draw conclusions that allow us to generate systems that allow for a high probability of forward trading profit with only IS information. I try to be as thorough as possible – and I will take any advice you have for me to improve – although sometimes I don’t make blogposts exceedingly rigorous :o) Thank you very much again for posting,
Best Regards,
Daniel
Thanks for the detailed explanation. You wrote that
“A part that I didn’t publish here – which perhaps is what you’re missing – is that the sum of all OS results (profitable and losing ones) is always positive and becomes more positive as the IS size grows larger. This unequivocally demonstrates that the system generation process gives a larger OS edge as the in-sample size grows bigger.”
I disagree. This may be an indication that the IS and the OS are becoming identically distributed as the IS increases. In simple words, the more data you use in the IS, the higher the probability that the OS is a sample drawn from the IS. This is what your study shows actually and I am surprised again you fail to see that. Good Lord you are open to criticism. That is a huge positive.
In other words, nothing of the sort you described above indicates an edge but the simple fact that as IS increases the OS seems to becomes a sample drawn from the IS in your study or in even much simpler words the condition found in the OS are included in the IS. Consequently the outcome will be positive and if you or anyone else does not realize that then he is fooled by randomness. When the market generates a sample that is not identically distributed and the distribution if returns changes the results will change often for the worse. I think you have been fooled by randomness with the kantu project. You may want to retain the positive aspect of this comment.
Hi Rick,
Thank you for your reply :o) I certainly agree with your conclusion here, obviously it simply indicates that the probability of the OS being a part of the IS grows larger as the in-sample size becomes larger. However since this has been drawn from a wide variety of randomly distributed IS-OS pairs it indicates that there is a tendency for part of the IS behaviour to at least partially represent the OS along a wide variety of market conditions. If you define an edge as an ability to get statistically relevant results above random chance from forward testing performance (meaning that you find a way to predict OS performance based only on IS variables) then I believe this study proves that historically there is a bigger edge as the IS size grows larger.
Obviously I agree with you in that when the market generates a sample that doesn’t follow the same rules then the above assumptions will fail. However the analysis showed that historically the market has had OS performance matching at least part of the characteristics of the IS under a wide variety of randomly chosen IS-OS pairs, isn’t it a rational assumption to consider that this behaviour is bound to continue going forward? I believe that the fact that historically we have observed OS behaviour to match the IS (again under a wide variety of randomly chosen paired windows) and the like-hood of this happening increases with IS sample size shows some significant characteristic of the market.
In the end it is obviously a construct based on past market data and obviously eventually prone to failure as every other trading implementation/methodology also is. However I fail to see how the above behaviour could be attributed to randomness as if you generate random data (which I have done a test with) you will not be able to find the logarithmic trends that I describe on the post. If this characteristic of the market (that the probability of the OS market conditions being part of the IS increases with sample size and that OS profitability relative to IS results also do) was random, I would definitely find the same trend with randomly generated data and I would be able to get similar or equal OS profits (which I don’t). In any case, I am open to any suggestions you may have (any tests, etc) to add further value to this study. Thanks again for commenting :o)
Best Regards,
Daniel
” If this characteristic of the market (that the probability of the OS market conditions being part of the IS increases with sample size and that OS profitability relative to IS results also do) was random, I would definitely find the same trend with randomly generated data.”
I never said it was random, actually quite predictable it was. “Fooled by randomness” means attributing characteristics to to randomness as you have done. The characteristic you attributed does not allude to an edge in my opinion but to normal behavior of price series. Also I never said that this should be present in random data. I said that this behavior is not describing an edge as you claimed. What you think is an edge is a quite predictable phenomenon. Thus you cannot deduce from it that using more data will increase the edge. You have only proved that using more data will increase the number of systems that are profitable in randomly chose IS-OS.
Hi Rick,
Thank you for your reply :o) It is also worth noting – although not in the post – that the sum of the absolute profit/loss of the OS period for all systems also increases as a function of sample size, therefore I would say that the edge does increase as the in sample size increases as the profit achieved if all systems were traded would be larger. Wouldn’t you agree ? let me know,
Best Regards,
Daniel
PS: If this was characteristic of price series it would happen for all symbols across all markets, this is not the case!
Another question that comes to my mind when reading this is the whether or not the scale of the data would illicit the same logarithmic scale. For instance if the strategies are build on the daily time frame and a good amount of OS data is 3000 days, would the same be true for an hourly system (3000 hours)?
As the OS data becomes greater and as the number of profitable systems become greater, how does the average profit per system compare? Is there a point that the systems become to generalized to handle all market shifts and the average profits start to decline, or does the increased OS data make the average profit increase?
As per Josh’s post, I too am interested if these thresholds (3000 periods) and the logarithmic relationships apply for smaller timeframes (H1, H4).
Perhaps the daily timeframe holds more significance because it contains a broader range of information (such as multiple announcements) as opposed to smaller timeframes (H1), many periods of which may contain more market noise.
What are your thoughts?
‘… that the sum of the absolute profit/loss of the OS period for all systems also increases as a function of sample size…”
But of course…longer IS -> more spurious correlations -> more signals in the OS -> more profit in the OS for the profitable ones. I think your concept of an “edge” is highly flawed. Edge does not mean more profit in the OS and it does not mean more systems pass OS.
“If this was characteristic of price series it would happen for all symbols across all markets, this is not the case!”
That is exactly what I said. That was a particular characteristic of a particular price series. The fact that it is not the case across all markets means that you were fooled by the randomness of a particular price series.
I have a suspicion that this kantu program will generate heavy losses for those who use it because it makes it so easy to get fooled by randomness and use spurious correlations. I think it is not an issue here how people use it. The concept it inherently flawed. I am surprised how you got so involved in this dubious concept. Of course, that is your prerogative.
Hi Rick,
Thank you for your reply :o)
It is not only more profit in the OS for the profitable ones, it is the sum of ALL the OS results (both profitable and losing ones) so there is even a reduction in the losses of strategies that were losing in the OS with smaller in-sample sizes.
I am puzzled by how you define an edge. I would define an edge as an ability to obtain profits above random chance under unseen market conditions. Isn’t this what we are seeing here? There is an above random chance historical probability to obtain profits under unseen market conditions for strategies generated using only IS data on the EUR/USD. If this is particular to this pair how does this make this being “fooled by randomness” ? A characteristic that is derived from an exhaustive long term analysis of a pair, based on randomly chosen IS/OS pairs involving thousands of randomly generated IS profitable strategies is hardly something that is random. There is no spurious correlation here, if you rerun the tests using 10K systems generated across random IS/OS pairs you get a very similar result. This means that this is a clear characteristic of this pair, I would say that if the pair has worked like this for the past 25 years then assuming it will continue to behave in this way is not a terribly bad assumption (would you disagree?). If you cannot use historical behaviour to draw some parallel to allow you to design systems then how do you test if you have an edge? Also as I mentioned on earlier comments this characteristic is not easily exploitable and this requires far more research into the matter.
You are clearly entitled to your opinion about the program and how it may or may not work for those who use it. I will just say that if you want your criticism to be constructive I would sincerely appreciate it if you would also suggest (or at least hint) to solutions to the problems you mention rather than simply mention them in a manner that simply doesn’t do much more than say you think it isn’t the right way to do things. Hey I am always open to criticism, but this is only useful for me if it is constructive in nature. There are also many more projects I am working on, I never put all my eggs in one basket :o). Thanks again for commenting Rick,
Best Regards,
Daniel
Thanks for your responses.
“I would define an edge as an ability to obtain profits above random chance under unseen market conditions.”
But if this is the definition, you have not proved that the kantu systems can do better than randomly generated systems on the same data. I guess that was not the objective of the study but we came to that point through the discussion of the IS size. The argument was that your conclusions about IS size were due to the specific randomness in the particular sample. You admitted that by saying that you got these results only for that series. But along the way, you called that an edge. This means that one of your objectives was not only to show that longer IS is preferable but to claim that the systems that indicated that had an edge. I pointed out to you that the more data you use the more profitable OS you will get by design and that is not necessarily an edge because it may just happen that the OS in this series was drawn from the IS something that can change in the future and usually changes.
I think my argument was clear. Your answers I am afraid to say are a bit confusing. You first admit that these results are pertinent to only one price series. Although this immediately implies a curve-fit of some kind you call that an edge based on the vague definition above.
“If you cannot use historical behavior to draw some parallel to allow you to design systems then how do you test if you have an edge? ”
That is not what I said I am afraid. One key aspect here is to check how many of these thousands systems you generate are essentially equivalent. You have not done that and this is a basic step otherwise your results hide multicolinearity. I suspect about 80% of the systems are virtually identical. I am sorry but I have no more time to spend on this subject and I thank you for your replies but in my opinion your analysis is seriously flawed and your conclusions are unfounded. Thanks, bye.
Hi Rick,
Thank you for your posts and for the interesting discussion :o) Hope to see you around,
Best Regards,
Daniel
Hi Daniel,
Interesting post all the way to the end. I agree on comments regarding OoS sample. Intuitevely I think that Oos needs to be larger than in-sample but also that both in sample and Oos need to be large enough to comply with all markets conditions we expect (hi/low vola, up/down/flat trending, etc)
So a good and rigorous approach is very appreciated.
Keep on with your great work!! :-)
Horacio