A key to the construction of better trading systems is the building of strategies with position management rules that are able to take advantage of luck and minimize losing trades. Such systems can be constructed using a wide variety of different mechanisms – like the trailing stops discussed within some of my previous articles – but in general the philosophy behind these exits is the same. What we want to achieve are strategies that can avoid giving back floating profits while giving trades move to grow and also preventing a move towards the worst possible case (the initially placed stop-loss value). On today’s post we are going to discuss a position management scheme that attempts to tackle these goals via the use of dynamic stop-loss values relying on time-based functions. During the next few paragraphs I will expose my ideas around this subject as well as some preliminary results I have obtained using the simplest implementation of this methodology.
–
–
What do you do if you want to take advantage of favorable movements and reduce the chances to reach the initial stop-loss given to your strategy? The most intuitive answer to this question is the trailing stop. As discussed in previous posts, the idea of a trailing stop mechanism is to move the stop-loss towards winning territory as the trade develops in our favor. A trailing stop mechanism keeps the stop-loss well behind price and ensures that it is given “room to move” if there are small unfavorable movements within a generally favorable run. What the trailing stop achieves is to prevent – at least in part – giving back as a trade moves into profitable territory. However the trailing stop mechanism – which we could define generally as a price based position management scheme – has a general problem when there is no favorable scenario.
When a trade develops straight against a trader the trailing stop mechanism lacks the tools to move the stop-loss because no favorable movement has been experienced. In this sense the trailing stop does not actually manage a position until there is a movement that takes us into positive territory. However it is obvious that if a trade does not move into positive territory the stop-loss should be in some way changed as the expectation of an unfavorable movement cannot be the same as on the signal bar. For example if you entered a trade and expected a maximum stop loss of 50 pips, this expectation of loss cannot be the same if after 20 bars price is now at -40 pips. Should we wait for price to reach the 50 pip stop-loss or should there be a way to compact the stop-loss to reduce the expectation of loss on a now almost certainly losing trade? Should the stop-loss be compacted ?
If we want to move the stop-loss in our favor as a trade develops then a way to do this is to use functional dynamic stop-loss mechanisms. These mechanisms move the stop-loss in favor of the trader as a function of time, trying to compact the trade to match a certain expected development of price action. Since this mechanism manages trades as a function of time there is no need to wait for favorable movements but we already know how a trade’s position management will evolve right after it is opened. The important thing here is to define the function that will determine the variation of the stop-loss as a function of time as this contains our expectations for price action evolution.
–
–
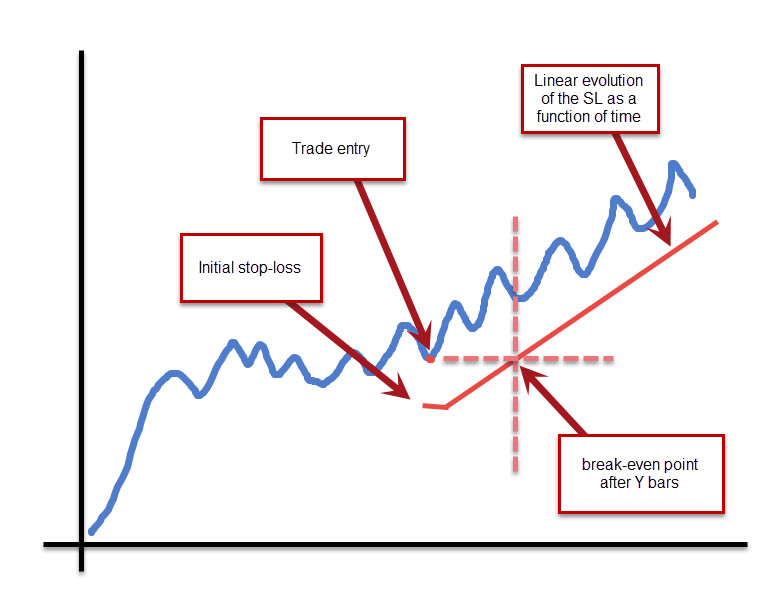
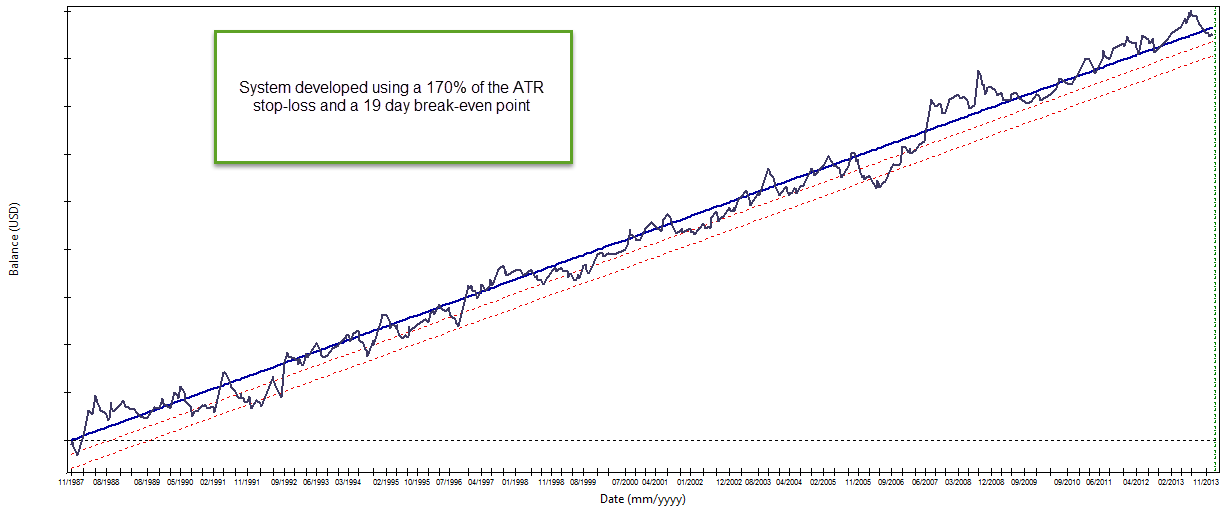
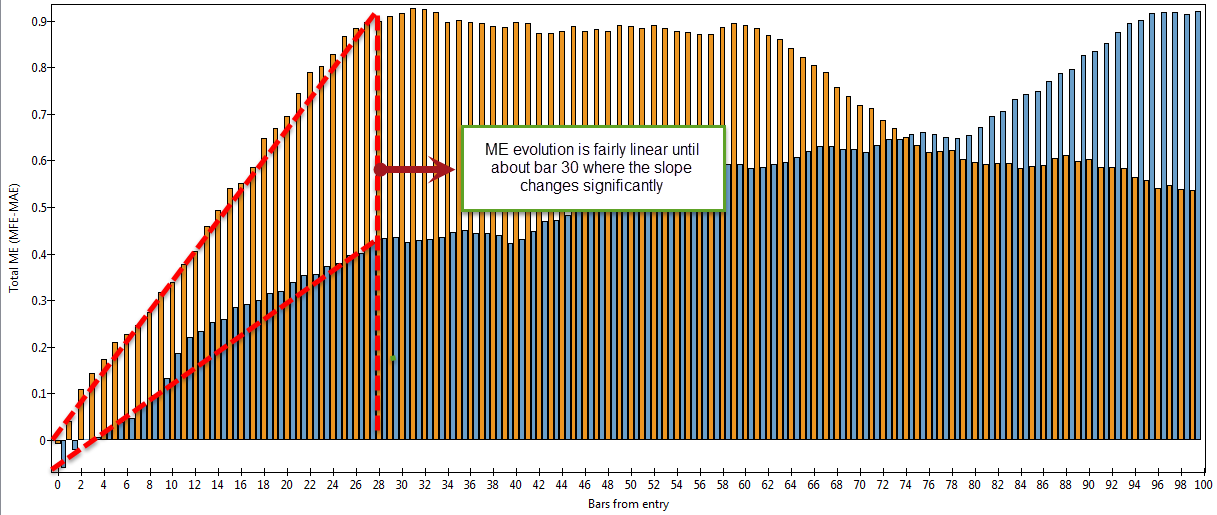
The simplest way to implement a dynamic stop-loss is to use a linear function whose only parameter needed for definition is the break-even point. If the initial stop-loss is set at X pips and we know that after Y bars the stop-loss needs to be at break-even we can then create a linear equation that passes through (0, SL) and (Y, 0), the stop-loss will evolve linearly from its initial value towards break-even after Y bars and then it will continue to evolve the stop-loss into favorable territory until the stop-loss is triggered by on-going price action. Notice how we are not limiting trade age but we are simply imposing an assumption of linear price movement after trade open that will always conform to a volatility which will be smaller than our stop-loss. The system showed above is an example on the GBP/USD daily chart of a system developed with an 170% of the ATR stop-loss and a 19 day break-even point. The system takes a total of 428 trades during the 25 year testing period with the average trade length being a bit more than a month. The mathematical expectancy for this strategy also conforms to the linear favorable movement assumption with a linear increase in the mathematical expectancy that becomes almost flat near bar 30 (which is also related with the average trade length).
Using data-mining we can create systems – like the above – where the entry signals generate trades that have the expectation derived from the exit criteria. This also agrees with the system development philosophy I have explained across previous posts where systems are developed to match a desired way to exit the market (not the other way around as it’s usually done). In this manner we can develop systems where trades are expected to evolve in a very specific manner, which is something that is difficult to do when data-mining is not used.
–
–
Finally I would like to point out that this is just the tip of the Iceberg, as time based stop-loss functions can be developed in all manner of ways. For example you can develop functions that are non-linear (quadratic, exponential, logarithmic, etc) giving you the possibility to attempt to find systems that match any desired expectation of price movement. I am in the initial stages of testing this position management using a linear approach but the next step is certainly to generate systems using more elaborate non-linear approaches. It is also worth mentioning that any additional parametrization used in the creation of this dynamic stop-loss mechanisms must also be taken into account in the calculation of data-mining bias. If you would like to learn more about system development and how you too can generate your own portfolio of algorithmic strategies please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading in general . I hope you enjoyed this article ! :o)





Hi, Daniel.
After reading the first paragraph of this post, Welles Wilder Parabolic SAR came into my mind. It adjusts stop loss in non-linear fashion, depending on whether market movement favor or contradict our position. However, it is definitely not profitable if used as standalone system.
I am looking forward on more of your development in the area of non-linear trailing stops. Keep it up! :)