The topic of system return correlations is extremely important as it forms the main pillar of successful portfolio building. Portfolio theory encourages us to put together different systems which are uncorrelated historically, such that our level of expected risk adjusted returns will increase as a result of an increase in compounding efficiency and an increased hedging of drawdown periods between strategies. However the building of portfolios based on historical returns is not so straightforward as the key assumption that historical correlations will match future correlations is often – if not always – entirely flawed. An increase in system correlations towards the future, especially under drawdown periods, leads to a higher than expected risk, which in turn eliminates the main advantage of portfolio building.
–
–
Given the above logic, it is important to find a methodology for portfolio building that combines and weights systems in a way that is more impervious to change than a simple analysis of historical correlations and a weight optimization towards an efficient frontier (a classic Markowitz portfolio optimization). It is important to find relationships that are more permanent than those derived from simple historical tests and then build portfolios that draw on these stronger relationships rather than the curve-fitted correlations we can derive from historical testing. Thanks to the combined efforts of several Asirikuy members (I would like to especially thank Jonathan for his ideas in this regard) we are developing a portfolio building methodology which I believe does exactly that.
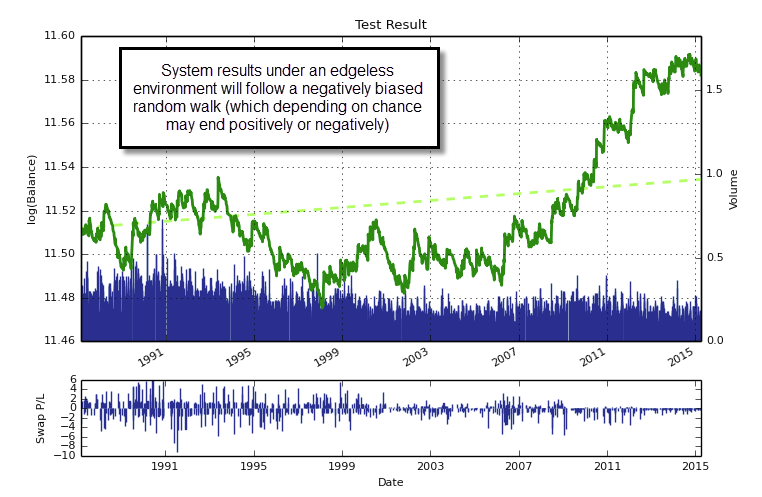
To go deeper into this I would like to first talk about the way in which systems correlate. When you analyse system correlations based on historical returns you are looking at correlations that are dependent on the inefficiencies that are being exploited by the strategies. If the strategies started to trade on an efficient environment these correlations might change in a way that becomes extremely unfavorable (which is what generally happens). In order to balance systems in a way that is independent of the inefficiencies within the historical data it is important to derive correlations that happen under an edgeless environment. We want to balance systems such that the portfolio is located at an efficient frontier under efficient market conditions (when we need them to hedge the most) while we care little about how they correlate under inefficient markets — which is when we are making positive returns.
–
–
In order to do this we simulate our strategies across random data sets (generated using bootstrapping with replacement from the original time series) and in this manner we derive system returns that happen under an edgeless environment (since the random series contains no causal past to future relationships). Of course the systems are mostly losers under this environment (we’re removing their edge!) but what we care about here is not their return but the manner in which their returns correlate. By performing the above procedure many times and then performing a markowitz optimization using the returns obtained from each run we can see what the overall portfolio weights are for each data run. We then know how the systems correlate when we have no edge and we therefore know what the optimum combination will be if the systems start failing. We are maximizing protection under a worst case scenario (an edgeless market).
–
–
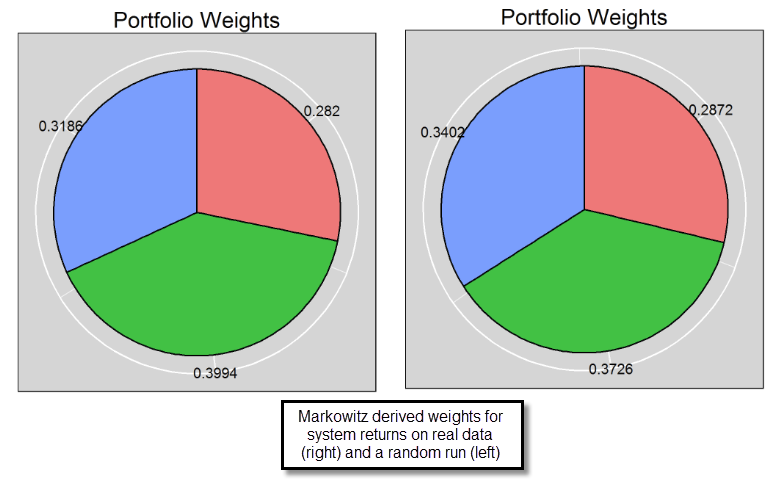
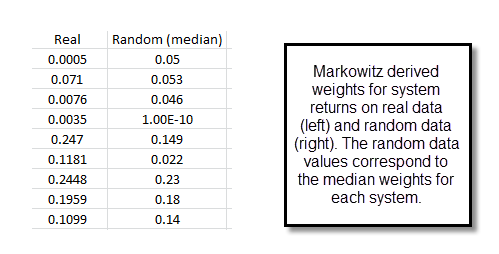
When the system correlations we have are quite robust we will see little change when moving to an edgeless environment (as seen on the second image, which compares the weights for a portfolio built with the same 3 systems with returns based from real and random data) while when we have significant distortions due to the presence of edges we do see very important differences between the random and real data markowitz optimizations. The third image on this post shows you the results for a 9 system portfolio where the median markowitz weights from random data runs do diverge significantly from those from the real data. For example we have a system that goes from 0.1181 to 0.022, showing that this system is particularly toxic to the other strategies under an edgeless environment.
Truth be told, we have no evidence yet whether the above method of building portfolios yields better results (we came up with it only a few months ago) but its construction based on results under edgeless environments promises to be more robust than the traditional construction of portfolios using weights derived from simple analysis of historical returns, optimizing weights to derive get to an efficient frontier. If you would like to learn more about our portfolio construction methods please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading.