Those of you who have read my blog know how much I have worked in the building of methods for system failure detection. Monte Carlo simulations have been a tool for this purpose during all this time but they suffer from several problems: they are often too slow at discarding systems and they are difficult to evolve as a function of time. During this past week I have given the issue of system failure detection using Monte Carlo simulations a lot of thought and in particular how we can use these simulations more effectively and evolve their expected worst cases with time in a manner that makes sense. Today I am going to discuss the problems inherent to Monte Carlo simulations and the solutions that I have come up with to allow for better failure detection using this method.
–
–
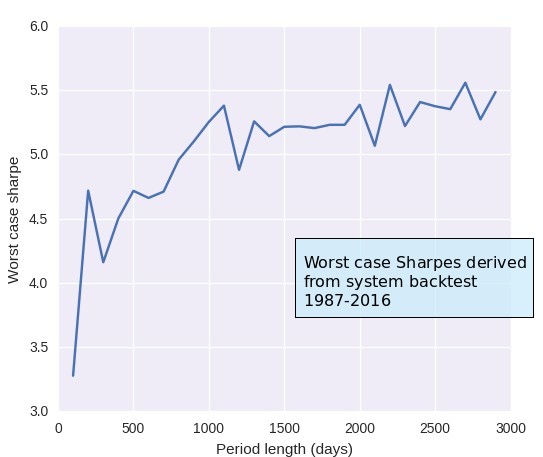
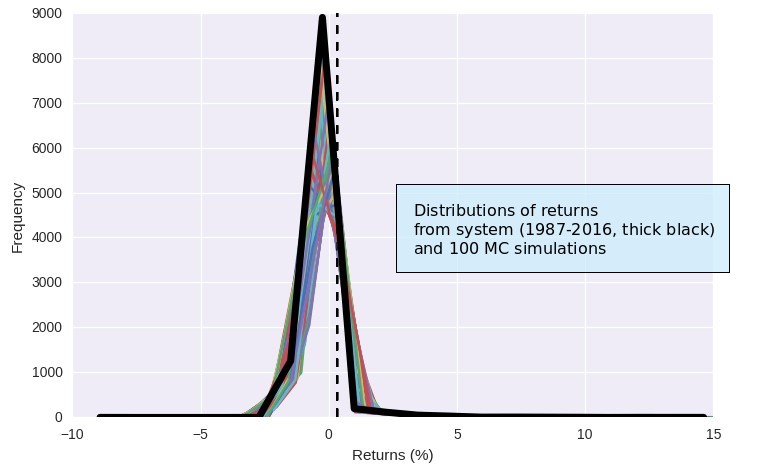
In Monte Carlo simulations we generate alternative equity curves of any given length for a trading system by making random draws from a trading system’s distribution of returns. The idea is that we can construct alternative plausible trading scenarios that share very similar distributions – all can be said to have come from the same source – but for which downside statistics are different. By building distributions for these statistics we can then locate thresholds that our systems should not breach if they indeed behave according to the trade distribution obtained from back-testing results. If 99% of all cases within our Monte Carlo simulations have a drawdown below 20% then we can discard our trading strategy with a 99% confidence if this drawdown level is breached. We know that the probability that our trading strategy is behaving as expected is below 1%.
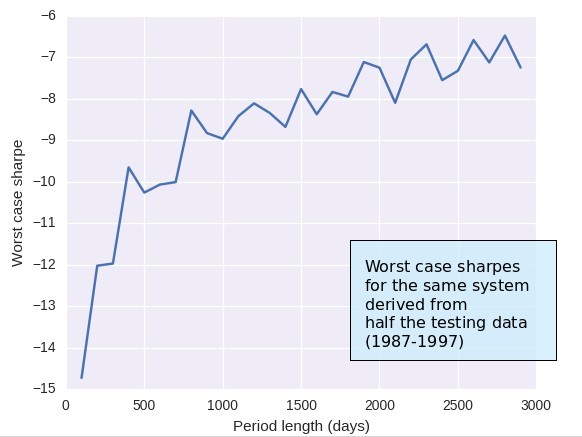
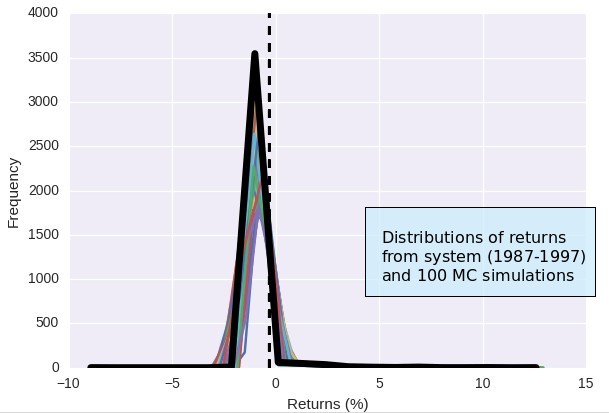
This simulation process makes several assumptions that are fundamental to its success. One of these assumptions is that the distribution of returns from the back-testing process represents the underlying distribution of returns of the system perfectly well. However we know that we can get easily fooled by this if we perform some simple experiments. If you create a random walk with positive bias as a system’s equity curve – sort of what we would expect a trading system to behave like – and you evolve it for some time you will see that the distribution of returns at points A and 2A are quite different. If you had performed Monte Carlo simulations at point A to draw worst cases they would not be valid at point 2A, which means that you would be working on wrong data. Inevitably if you define your worst case thresholds at point A and you trade forward indefinitely you will probably hit your worst case, even if the system never behaved badly. The problem wasn’t that the system was behaving wrong, it’s that you didn’t have an adequate measurement of the underlying process.
–
–
In order to use Monte Carlo simulations in a way that is useful you need to adapt your worst case thresholds as more data comes in. However this creates a problem dealing with the worst case threshold because if you keep on adapting your worst case targets as your trading evolves you will simply never hit your worst cases because deeper and deeper draw-downs will become a part of your distribution of returns and hence will become a plausible and probably a common case in the Monte Carlo simulations. So you cannot simply perform Monte Carlo simulations after every trade to update your simulations because then you’re always sort of expecting what you’re getting, there is no way that you would hit a worst case.
The solution to the above problem is simple. Every time you will be trying to detect system failure you will be within a drawdown period and you don’t want to update your statistics then. buy Neurontin 100mg The problem is solved by evolving your Monte Carlo simulations only when a trade that marks a new balance high is made. You update your simulations whenever you’re making new highs – meaning the system is performing as you want it to – and when the system is within a drawdown period you’re not updating but simply trying to detect failure according to the statistics you derived within the last update. This methodology ensures that your Monte Carlo simulations are always using the most recent accurate estimates of the underlying process but yet they do not update when you’re detecting failure and therefore keep their usefulness as a worst case detection mechanism.
–

–
This simple change to the Monte Carlo worst case evaluation process makes it instantly more valuable for failure detection. We now have a method where the worst case thresholds are updated as we get more information pertaining to the underlying process guiding our system while we still retain our ability to detect system failure. This is all obtained simply by evolving all worst case detection thresholds while we are reaching new equity highs while we avoid updates when a system is going through a downside scenario. If you would like to learn more about system failure detection and how you too can learn how to trade while properly evaluating whether your trading strategies are working as expected please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading.




