Mechanical Forex

During the last few posts we have been discussing reinforcement learning in Forex trading and it’s potential for the development of trading systems. After these posts it should be apparent that the most important issue with reinforcement learning – given its great power to learn from the data – is actually curve-fitting bias. Today I want to go a bit deeper into this curve-fitting issue and how we can actually predict whether a given reinforcement learning approach will or will not generate a usable trading algorithm. For this we will use some samples taken from my experiments with the same bullish/bearish state based Q-learning system I have used in the past couple of posts I’ve written on this subject.

–

–

In my last post we saw how increasing the degrees of freedom in reinforcement learning can affect the way in which the system performs under a pseudo out-of-sample period. From this it may seem that the best solution for the curve-fitting problem is simply to perform an in-sample/p-out-of-sample split and train the Q-learning approach on in-sample data while you evaluate the results within the pseudo out-of-sample data but this approach has some very important weaknesses that make it of limited usefulness. Since the pseudo out-of-sample data is always the same you get a lot of bias related with multiple testing, since you’re able to modify your Q-learning approach until it simply works on the pseudo out-of-sample, but it might just then work in the pseudo out-of-sample by chance – due to the data-mining bias you have introduced – and may fail across others. Is there an approach not subject to this multiple testing problem that could predict a given reinforcement learning setup’s potential?

Actually there is a way to do this. Since we want the Q-learning approach to only learn from information that is caused by market inefficiencies and not just by noise we can use data where there is only noise to see how successful our Q-learning algorithm can be. We can generate a time series using bootstrapping with replacement from the original data series in order to create a time series where there are absolutely no inefficiencies present since the returns have been randomly shuffled. If we apply a Q-learning algorithm to this random data we will be able to see how much information our algorithm is learning from noise and when we compare this to the amount of learning we can do on real data we can get a sense of how much we are actually able to get learning beyond what is expected from just the data-mining power of our learning algorithm.

–

–

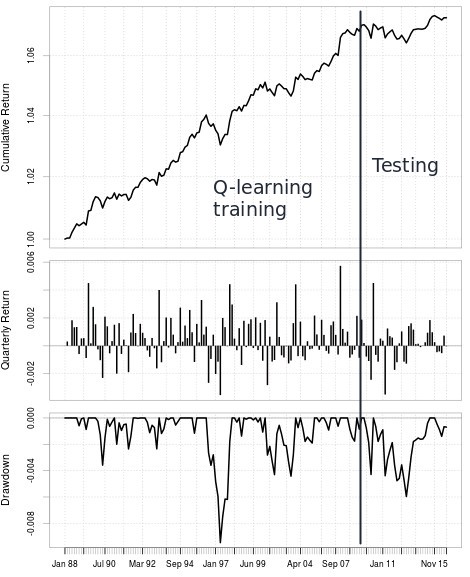
The results in the first graph within this post show you exactly what happens when we perform this exercise using a Q-learning algorithm that learns from 8 or 9 past bar directions. As you can see both are able to learn substantially from the random data and increasing complexity from 8 to 9 bars does mean that we are able to extract more useless information from noise. However what is most interesting is that the difference between the learning using random data and the learning on the real data is the same for the 8 and 9 bar cases. This means that when you increase the number of bars in this case from 8 to 9 you’re gaining no new knowledge and you’re just getting more “fit from noise” that does not imply you’ll receive more profit. This goes perfectly well from what we learned from doing pseudo out-of-sample tests in my last post. The 7, 8 and 9 bar Q-learning exercises have virtually the same results in the pseudo out-of-sample and that’s because the difference between what is learned from noise and what is learned from inefficiencies is the same in the three cases. We can learn this from learning on random data without ever doing pseudo out-of-sample tests.

Random data gives you a very useful tool in this case because you now have a way to evaluate your Q-learning algorithm that has no problem with repetition. You can generate trillions of random data series and therefore you can test how well you learn from noise as many times as you want. If you’re able to increase the difference between what you learn from noise and what you learn in the real data then you’ll be able to get algorithms that have a much better chance at succeeding under new market conditions as the information they have learned from the market will be much more relevant for profitability. By modifying the Q-learning approach to expand this difference I was able to improve results to get the second image showed above. These results are much better and contain a pseudo out-of-sample that is a much better match to the in-sample period, note that I never used this pseudo out-of-sample within the modification process but just to showcase the result and why pseudo out-of-sample testing is not needed to improve a Q-learning approach.

–

–

Of course the above are just some initial steps in Q-learning and reinforcement learning in general but now that we have established a way to quantify how good a Q-learning approach might be (that is not simply historical testing) we can now experiment with modifying Q-learning and see what we get when we do different things. What if we used heiken-ashi bars? Indicators? What if we gave Q-learning the same information a human usually looks at? These are some of the things we will look into in future posts. If you would like to learn more about machine learning in trading and how you can create systems that constantly retrain  please consider joining Asirikuy.com, a website filled with educational videos, trading systems, development and a sound, honest and transparent approach towards automated trading.strategies.